
Have you ever wondered if ST Math adapts to the learning needs of students?
By adapt, I mean is ST Math designed to provide students the opportunities they need to develop and grow as they engage in the learning process? Is the curriculum in ST Math designed to provide students with content and experiences that will help students build learning schemas, or understandings of concepts? Does the content provide an opportunity to meet them where they are and scaffold the instruction they receive to help them develop deep understanding?
ST Math meets students needs at the point of learning through informative feedback and rich visual models. ST Math does not adapt in the sense that it changes as the students play, based on some algorithm that provides them with a lower level problem, when they were not able to solve the first one.
Instead it uses neuroscience principles of learning to engage the student in the brain’s natural process of adapting and learning. As students play ST Math puzzles, the rich, visual models and the informative feedback allow students to “see” the math, learn from their mistakes, and adjust their thinking.
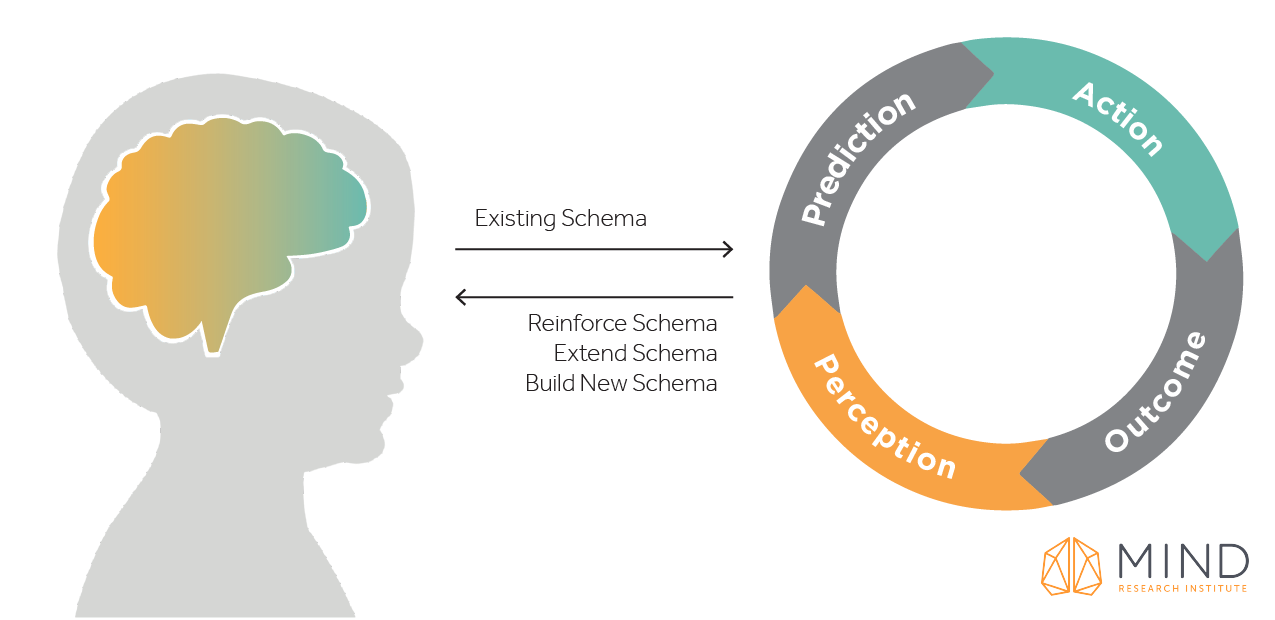
When playing ST Math, students learn to adapt at the point of learning. This happens because the type of adapting I am talking about is natural, authentic, and done through the learning process by the student. It is not reliant on computer algorithms, but instead leverages what naturally occurs in our brains known as the perception-action cycle.
Essentially, our brain makes sense of the puzzles in the games by creating and testing hypotheses about the way the puzzles work. When presented with a puzzle, our brain makes predictions based on past experiences and knowledge. We then take action based on our hypothesis. Our brain perceives the results of our action through the immediate, informative feedback and uses the learning from the feedback to adjust our hypothesis.
ST Math uses visual, spatial-temporal models and immediate, informative feedback to engage students in the perception-action cycle. Through the feedback, students not only learn what was wrong, but they learn how to adapt their strategy, ideas, and understanding to build new learning. Students develop their math skills as well as important life skills (e.g., perseverance, accountability, problem solving, and agency).
Using visual models to develop math concepts provides students with access in a way that words alone do not. Take for example a problem like 3 ⅓ - 2 ²⁄₆ . For many students who do not have a solid understanding of fractions, they may see a problem like this and not know where to begin. Potential barriers might include lack of understanding around mixed numbers, unlike denominators, and/or subtraction of fractions.
What if you could provide not only access but equity by maintaining the rigor of a task like this for your students?
Suppose some students in a fifth-grade class are still struggling with understanding unit fractions, others are struggling with fraction equivalence, still others are struggling with understanding fractions and their value as numbers, but your curriculum has you teaching adding and subtracting fractions with unlike denominators.
This is where ST Math visual models are so powerful because they can provide students an entry point into the grade-level puzzle.
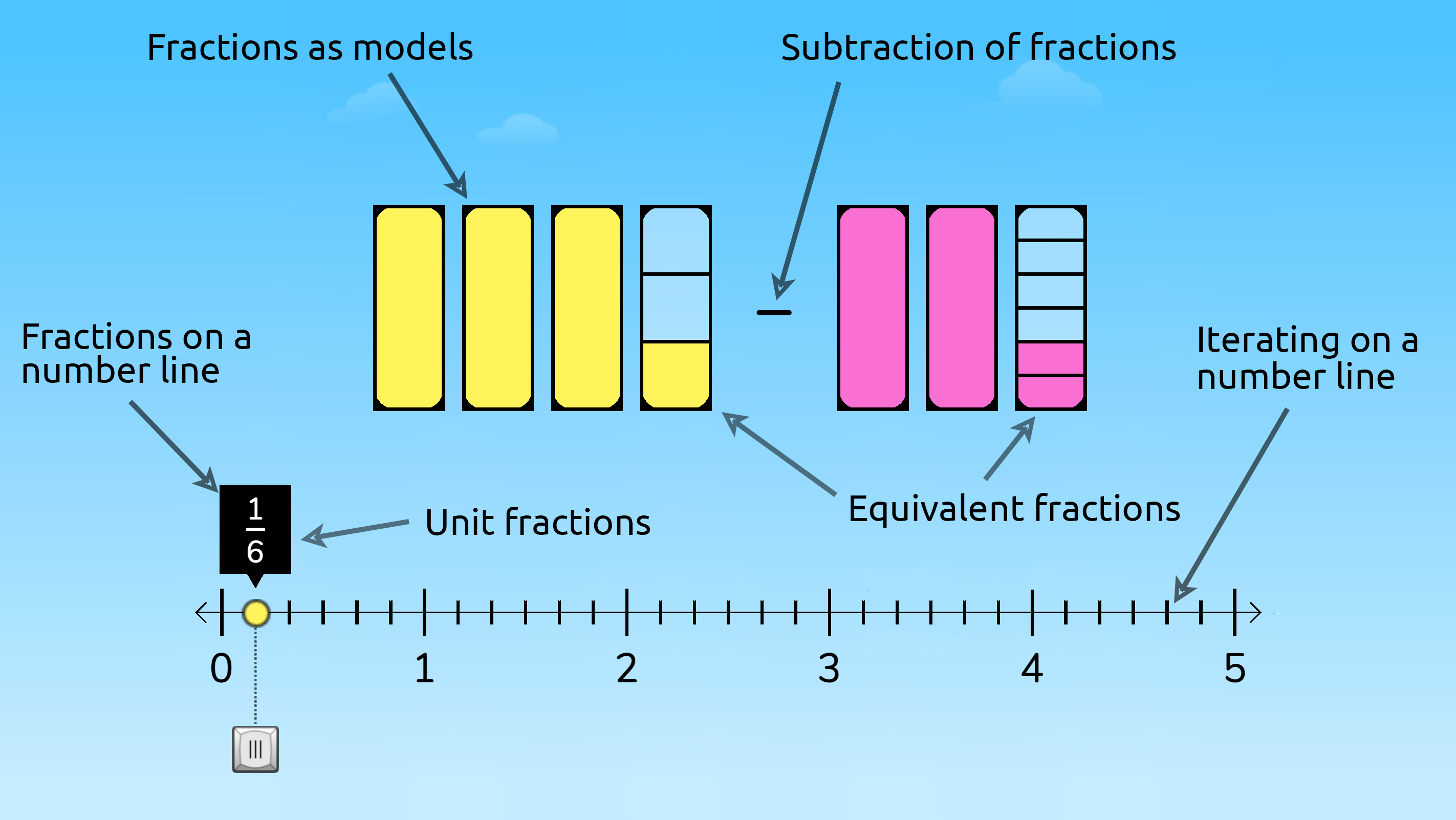
The ST Math game Scale Fractions is a great example of using a visual model to solve the problem given above: 3 ⅓ - 2 ²⁄₆. The students who did not know where to begin with this algorithm now have an opportunity, through the visual model, to access the mathematics.
This image from the game Scale Fractions shows several math topics that are potential entry points for struggling students.
For example, a student may use their understanding of equivalent fractions (which may be a lower grade level skill) to gain access to the grade-level problem presented in the puzzle. As students play, they work through the perception-action cycle building on their understanding of fractions, processing the feedback, and adjusting their thinking. Students are actively developing their understanding of the grade-level content and connecting mathematical ideas.
Students playing grade-level material see the objectives their classmates see, however they will move through the puzzles at their own pace. In this model, students will get the opportunity to develop conceptual understanding, practice, and apply their learning by working through as many puzzles as needed to achieve 100% mastery of the content.
Instead of the program adapting the content, students are adapting in regard to the approach they take to solve the puzzle, strategies they use, and the way they are thinking about the concept. When students play ST Math they are getting more than a math program, they are learning that they are capable of taking on challenging grade-level problems, thinking them through, and achieving success.
You can now play sample puzzles from the new ST Math on our Play page. This includes Scale Fractions, mentioned above. For the best experience, the latest Google Chrome is recommended for ST Math games. Try Scale Fractions for yourself!
This sample puzzle above is not currently optimized for phones.
For best results, open on a computer or tablet.
Byrd, Christine. What the Perception-Action Cycle Tells Us About How the Brain Learns. [Blog Post] Retrieved from https://blog.mindresearch.org/blog/perception-action-cycle

Twana is Vice President of Curriculum and Instruction at MIND Research Institute. Follow her on Twitter @TwanaYoung.
Comment