Concept, (n.) \ ˈkän-ˌsept \:
an abstract or generic idea generalized from particular instances
Conceptual (adj.) \ kən-ˈsep-chə-wəl \:
of, relating to, or consisting of concepts
Understanding (n.) \ ˌən-dər-ˈstan-diŋ \
a : the power of comprehending
especially : the capacity to apprehend general relations of particulars
b : the power to make experience intelligible by applying concepts and categories
Like many educational buzzwords, conceptual understanding is one that has been defined in enough different ways that it starts to lose meaning. The focus of many conversations around conceptual understanding is also shallow, focusing on the idea that students need it, and less about how it is actually acquired. Which is unfortunate, because the “how” is the most important part. So we’re going to talk about the “how,” because having a deep conceptual understanding of math concepts is critical for problem solving success.
But just so we don’t gloss over the “what,” let’s clarify our working definition of conceptual understanding. As we saw in our dictionary definitions above, concepts are ideas generalized from particular instances, and understanding is making sense of experiences by seeing the relationships between concepts and applying them. So we could say:
Conceptual understanding in math is the creation of a robust framework representing the numerous and interwoven relationships between mathematical ideas, patterns, and procedures. This framework can be used to coherently integrate new knowledge and solve unfamiliar problems.
The key to developing the robust framework we mentioned above can be summed up in one word: schemas.
We’ve talked about schemas before—blueprints that describe an object, a string of events, an idea, or really...anything. From a neuroscience perspective, conceptual learning requires building schemas.
Schemas are neural networks, and the way those networks get created and connected ends up defining your concept, or understanding of the topic. And when we talk about having “deep conceptual understanding in math,” we’re talking building schemas of mathematical concepts that give students the ability to solve problems they haven’t seen before.
Not only do today's standards speak to the need for students to build conceptual understanding, the newer assessment problems require it. Here’s just one quick example of how older assessment questions tested students’ knowledge of volume, compared to how more recent ones assess that same topic.
OLD
.png?width=258&name=rigor-example1%20(1).png)
NEW
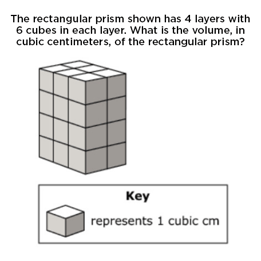
As you can see, the problem on the left (the old one) essentially provides the key to the solution. Just plug the numbers into the algorithm. In contrast, the problem on the right not only requires a deeper understanding of volume, but also allows students to solve that problem in multiple ways.
Whereas the older assessments would provide a series of questions in which the same problem solving approach could be used over and over again, newer assessments also vary the problems to test for conceptual understanding. This newer volume question is completely different than the rectangular prism one above:
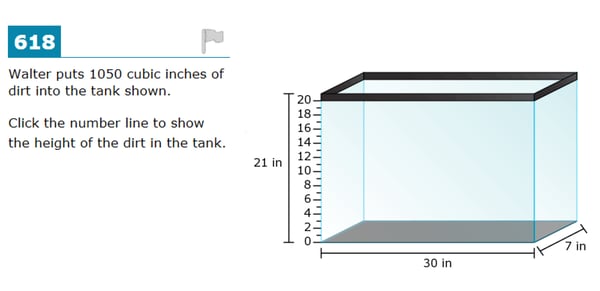This is a great, because we know that memorizing rules and math facts is not as effective as learning through creative reasoning. In order to solve new and non-routine problems, students must have robust schemas built for the underlying math concepts.
We talked earlier about how schemas are the key to deeper conceptual understanding. So the real question then becomes: how do we help students build schemas?
Rather than teaching math as a series of isolated concepts that students compartmentalize into rigid sets of rules and procedures, we want them to consider concepts as they relate to one another:
One example of building conceptual understanding is the approach visual instructional program ST Math takes, by teaching foundational concepts visually, then connecting ideas to symbols and language.
The puzzles in ST Math utilize a variety of visual models to present math concepts in non-routine ways. This approach allows students to build schemas quickly, as they interact with and manipulate models, and receive immediate, informative feedback. They see their choices play out, and can adjust their approach to a problem by incorporating that feedback, through the perception-action cycle.
The program requires students to think outside the box and creatively apply what they have learned to solve challenging problems. Many puzzles allow multiple solutions. As a result, students experience autonomy as they learn to transfer their knowledge at each increasingly rigorous step of the learning path.
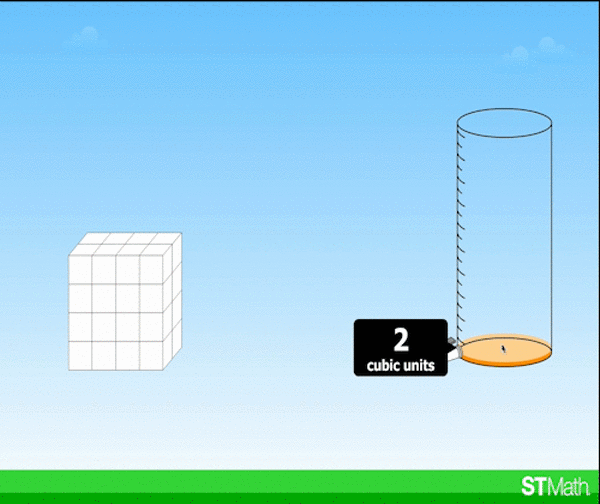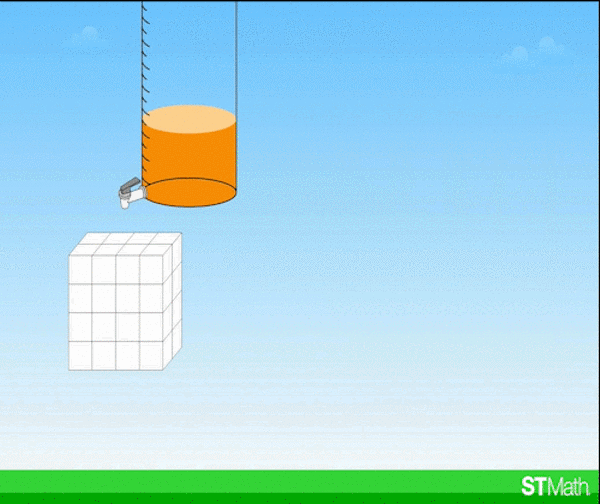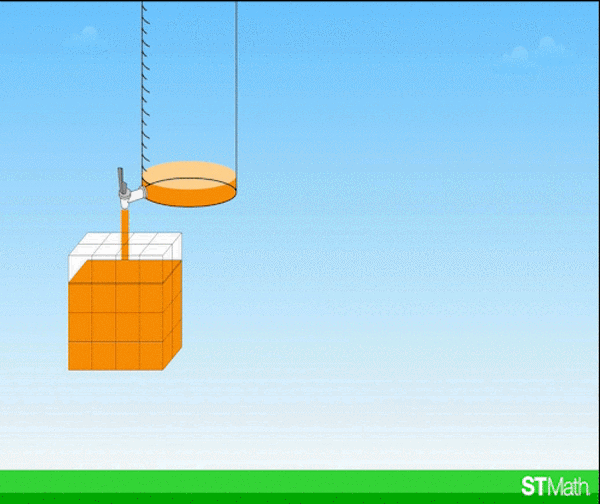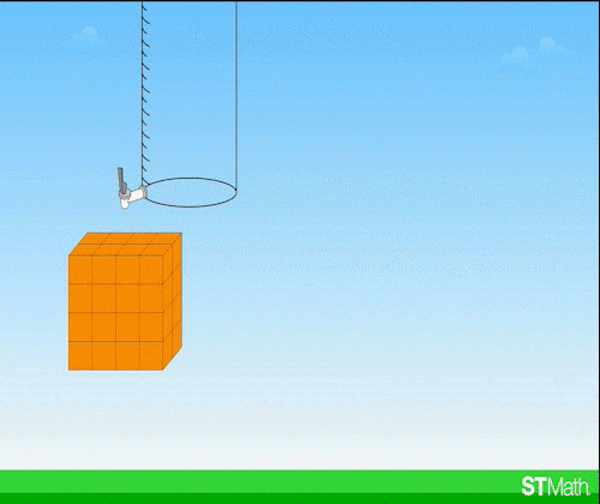
With these volume problems in ST Math, students can develop a schema for volume that goes beyond length x width x height, to develop a deep conceptual understanding that allows them to solve problems they haven’t seen before.
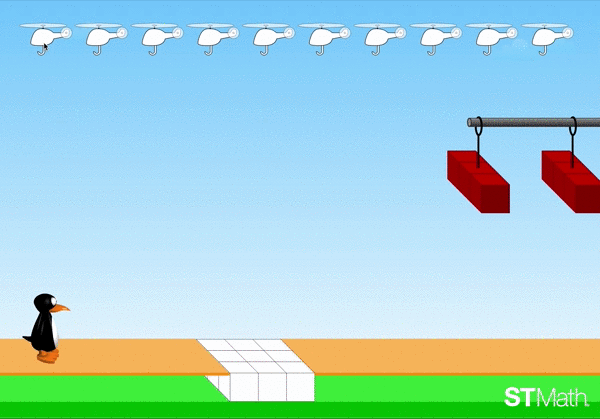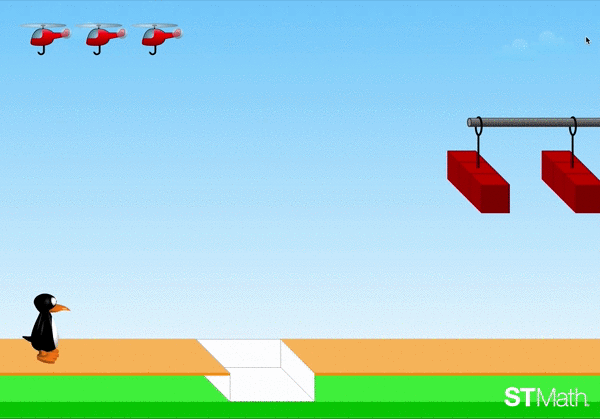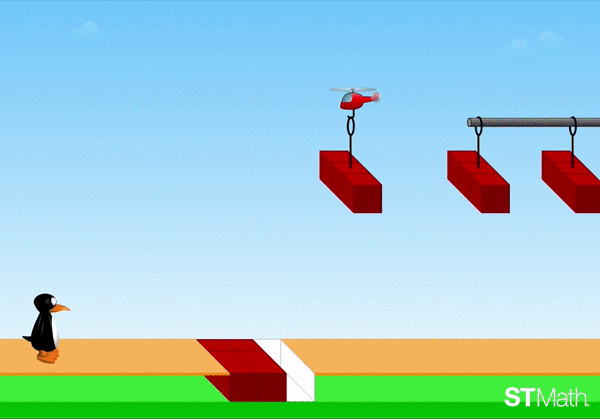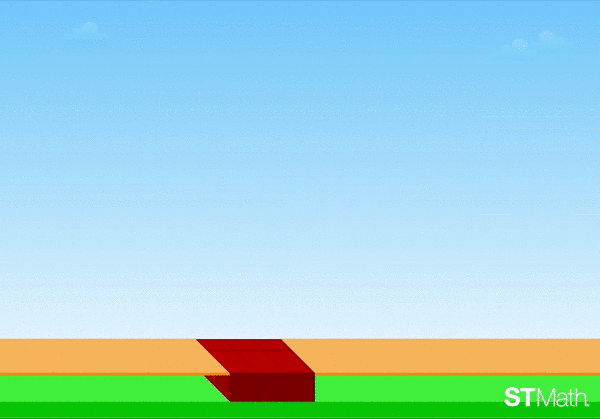
You can learn more about ST Math and how it supports deep conceptual learning, as well as experience some of the games yourself at stmath.com.
Want the latest from ST Math? Sign-up for our ST Math newsletter and be the first to hear about our offers and announcements.
Eric Sbar is Regional Vice President of West Partnerships for MIND Research Institute. He is a musician and educator, and enjoys connecting with math through nature while hiking, camping and sailing.
.png)
Comment