I’m sure you’ve seen all kinds of math memes floating around social media. They’re funny, but sometimes they get at fundamental ideas about mathematics education. Many of these memes are driven by the question which I’m sure you’ve heard someone say, “Why can’t we just teach math the way I learned it?”
And this naturally leads to an ongoing debate, “How do we teach math?” And it’s a good question, but to really answer it we need to change the perspective and ask ourselves something different: “How do we learn math?”
About 25 years ago, a group of neuroscience researchers from the University of California, Irvine, set out to find serious answers to this question by looking at spatial-temporal reasoning, its connections to music and creativity, and further connections to learning mathematics. Driving this research was the bold idea: What if math could be taught the way the brain learns? The result of this research was the program ST Math – the ST stands for spatial temporal.
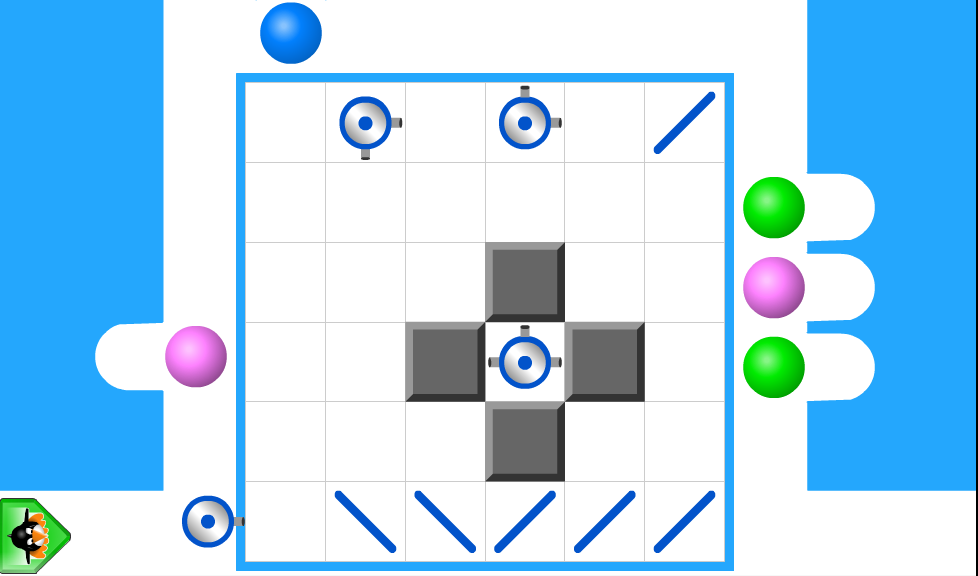
Spatial-temporal reasoning is the brain’s ability to manipulate objects in space and time to solve problems. In ST Math, the problem we’re always trying to solve is how to get JiJi the penguin across the screen. There are no written or verbal instructions. At the start virtually of any learning path in ST Math, everything is visual. This means that there is no barrier to learning – students engage by testing out their ideas and learning from the feedback.
It’s worth taking a minute to explore the neuroscience at work in this fundamental brain learning mechanism, it’s called the perception-action cycle.
Whenever we’re tasked with solving a problem, we use our existing schema (literally neural networks we’ve already developed) to make a prediction, “Here’s what I think will happen.” Then, we take action and the consequences of our choices are revealed. We perceive the outcome, literally by seeing it, and inside the brain – in the hippocampus, a little part right in the middle – something very remarkable happens. The prediction we made is compared to our perception: here’s what I thought would happen versus here is what actually happened. If we are correct, our prediction and perception match, and the schema that caused us to make that prediction is strengthened. This is how we build schemas and conceptual understanding.
But learning doesn’t just happen when you get things right. Imagine a different schema fired up causing us to make a different prediction and take an action - choosing moves in the game - that are ultimately incorrect. The game takes our input and animates it out and again, we perceive the outcome, and we see that JiJi did not make it across the screen. In the hippocampus, our perception is compared to our prediction, but this time they do not match.
First, the hippocampus sends a signal that de-prioritizes that schema. So, the next time we see a problem like this, this schema is much less likely to influence our thinking. This is how misconceptions are rectified. But importantly, a second signal is also emitted from the hippocampus that tells the brain, “You need to learn something new—you need to build new schema.” The idea that students learn through their mistakes is based upon this fundamental neuroscience.
This is what happens in every single ST Math puzzle. To complete a single grade level of ST Math, students will solve several thousand of these puzzles. That’s a lot of learning by doing, of active participation in the learning process, of testing your hypothesis and seeing precisely why you got something right, or wrong. That’s a lot of schema building!
Another challenge we have when we think about teaching versus learning is that we’re very used to thinking of math as a list—a list of chapters or a list of standards. This is useful when we are putting information in a book or deciding in what order we are going to teach concepts in class, but this is not how the brain stores and uses mathematical ideas to solve problems.
The brain would store it as connected schema, where the topics are nodes of the schema, but equally important are the connections between all the nodes of the schema It’s no exaggeration to say that when we talk about someone having a good conceptual understanding of math, we literally mean they have a deep schema—a rich web of connections between these ideas that they can use to solve very complex problems. These connections do not often happen by accident—students make them when they experience learning that is explicitly designed to build them.
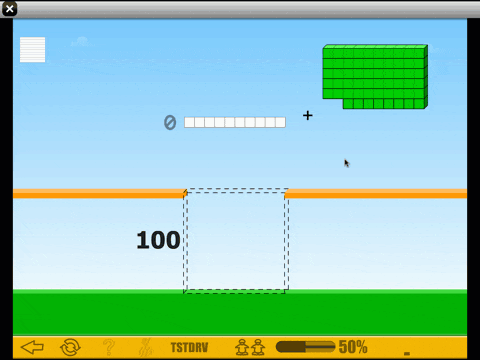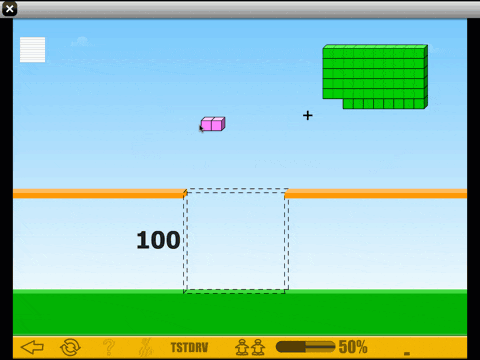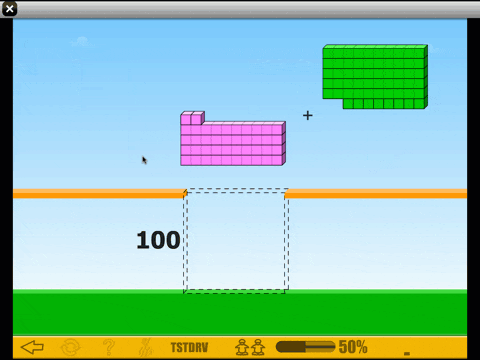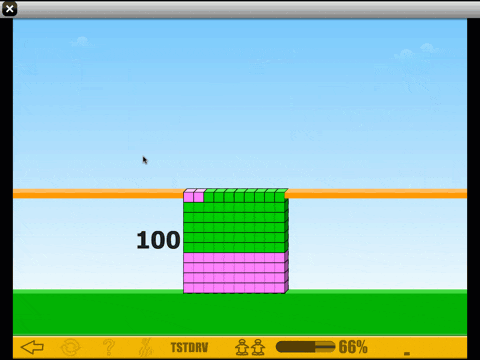
This brings us to the real power of ST Math. We want students to spend a significant amount of time working on math tasks where they need to use creative and critical thinking to solve non-routine problems. That’s easier said than done. First, the vast majority of curricular materials don’t consistently push students creatively to solve problems. That’s not to say students don’t need some practice of basic math ideas—they do—but that can’t be your only experience of mathematics. Second, in most curriculum, the only way we have of asking students a question is with a word problem. This is a barrier to entry for a large number of students. They get so lost in trying to decode the words that they never really tackle the underlying thinking. ST Math presents all problems visually, providing access for more students to creative thinking and non-routine problem solving.
A great and valid question at this point is: how does this conceptual learning methodology based on using spatial-temporal reasoning to build schema translate to outcomes on standardized tests? At MIND Research Institute, we have a lot of large scale data studies done on the efficacy of ST Math. Let’s look at these studies which are broken down by the effect of ST Math on different student subgroups.
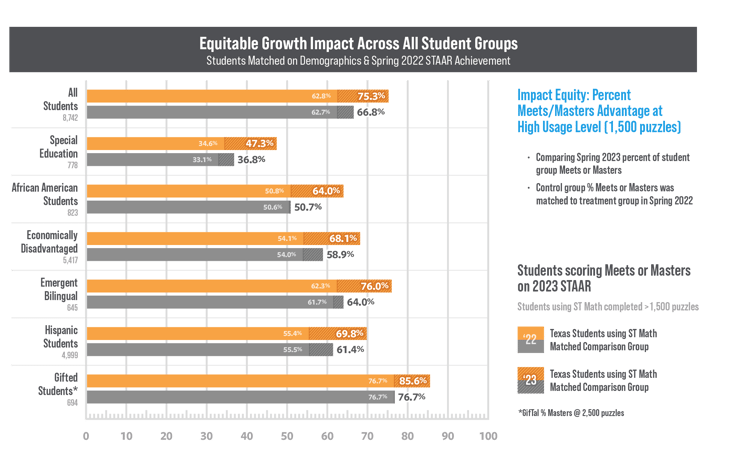
Percent of students meeting or exceeding standards in grades 3-5, 2022 vs 2023.
Find full reports here.
You can see that ST Math is not only highly effective for gifted students but for special education students, English learners, and all other student subgroups. ST Math is giving all students the chance to learn and think mathematically! It really is the cornerstone of an equity strategy—providing equitable access to learning tools proven to help all students.
To the students, this isn’t about neuroscience. They don’t know that it’s their perception-action cycle being activated. However, students do understand the idea of productive struggle: the idea that they are learning when they make mistakes and how powerful it is when they figure something out for themselves. In fact, last year, a peer-reviewed study showed something I’ve never seen before. The study found students who play ST Math have higher mathematics self-beliefs than non-ST Math students. By regularly playing this game with a little penguin, students began to see themselves as capable mathematicians.
This is fantastic! We know from other research that students—girls in particular—come to see math as something that’s “not for them.” But now, we have a tool to help students fight against the misguided belief that they are “not a math person.” We are all math people! We just need the right tools.
This brings us back to math memes. While they are funny and have a tendency to trivialize, they do strike at some important challenges in math education. For example, how should we teach multiplication, the old way, or the new way? But now we can look at this question through a new lens. We can examine different teaching methodologies from a schema-building perspective and we’ll see that they are designed to do completely different things.
The “old way” of teaching math is a beautifully efficient algorithm that will work no matter how large the numbers are. Practicing it will build up one node in your brain. It’s a method for speed and efficiency. The “new math” way is very different. It’s actually really cumbersome, time consuming, and a not very efficient way to multiply numbers together—but that’s not what it’s for. This new way of doing math is explicitly designed to build connections in the brain between different mathematical ideas, in this case, multi-digit multiplication and place value in order to build connected schema, and for that purpose it is really good.
The reality is we shouldn’t be teaching math the old way or the new way. What we need to do, and of course what we do in ST Math, is teach both. We use area models to build connections and conceptual understanding, and then we connect that to algorithms, speed, efficiency, and understanding.
So, how did we get here? Why is there this constant rift in mathematics education between teaching for conceptual understanding and teaching algorithms and procedures for speed and efficiency? I think the best answer can be found in this picture from the 1940’s.
You can see that it says, “Computing Division, Computing Section.” What’s important to realize is that the computers they’re referring to in this room are not the machines. The people here are human computers, paid to be fantastically good at doing math procedures with both speed and accuracy.
Within my lifetime, human computers were an integral part of getting us to the moon. But what’s fascinating is this line from a 1942 memo from the National Advisory Committee for Aeronautics (NACA), which later became NASA. It says, “The volume of work often necessitates computers (people) who can perform the routine machine operations (math calculations) with great speed, but who need not have much logical insight into what the results should be.”
NASA literally needed people who could do math with speed and accuracy but did not necessarily need conceptual understanding—and it wasn’t just NASA! Banks, insurance companies, etc. all needed human computers. Which is not to say that human computers were not fantastic mathematicians and problem solvers in their own right, many were, but even in more day-to-day jobs, there was just a need to be able to do math procedures quickly and accurately—it was genuinely necessary for everyday life. Being able to do math procedures quickly and efficiently was a valuable workplace skill.
This is the era during which most of our traditional textbooks were written and it is the ethos that still pervades the way we teach. But now, the chip in my cell phone can do more calculations in a minute than that entire room full of human computers!
The old way of teaching math was to make us do it like a machine, but the new way of learning math is to help us understand how it works so that we can build the machines.
There is a new currency in the world today—creative thinking and problem solving are the skills our students need. Employers are looking to find creative thinkers and, "Managers want fresh thinking and ideas that they can use right now to help them create value for their organizations and society." Creativity creates value. Computers—the actual mechanical ones—can complete the rote tasks.
And on the subject of creativity, researchers are consistently finding a strong link between spatial reasoning and creativity. Universities across the country are finding that incoming students' performance on the PSVT—a spatial reasoning assessment—is the best way to determine if students are ready for the creative rigors of today's STEM courses.
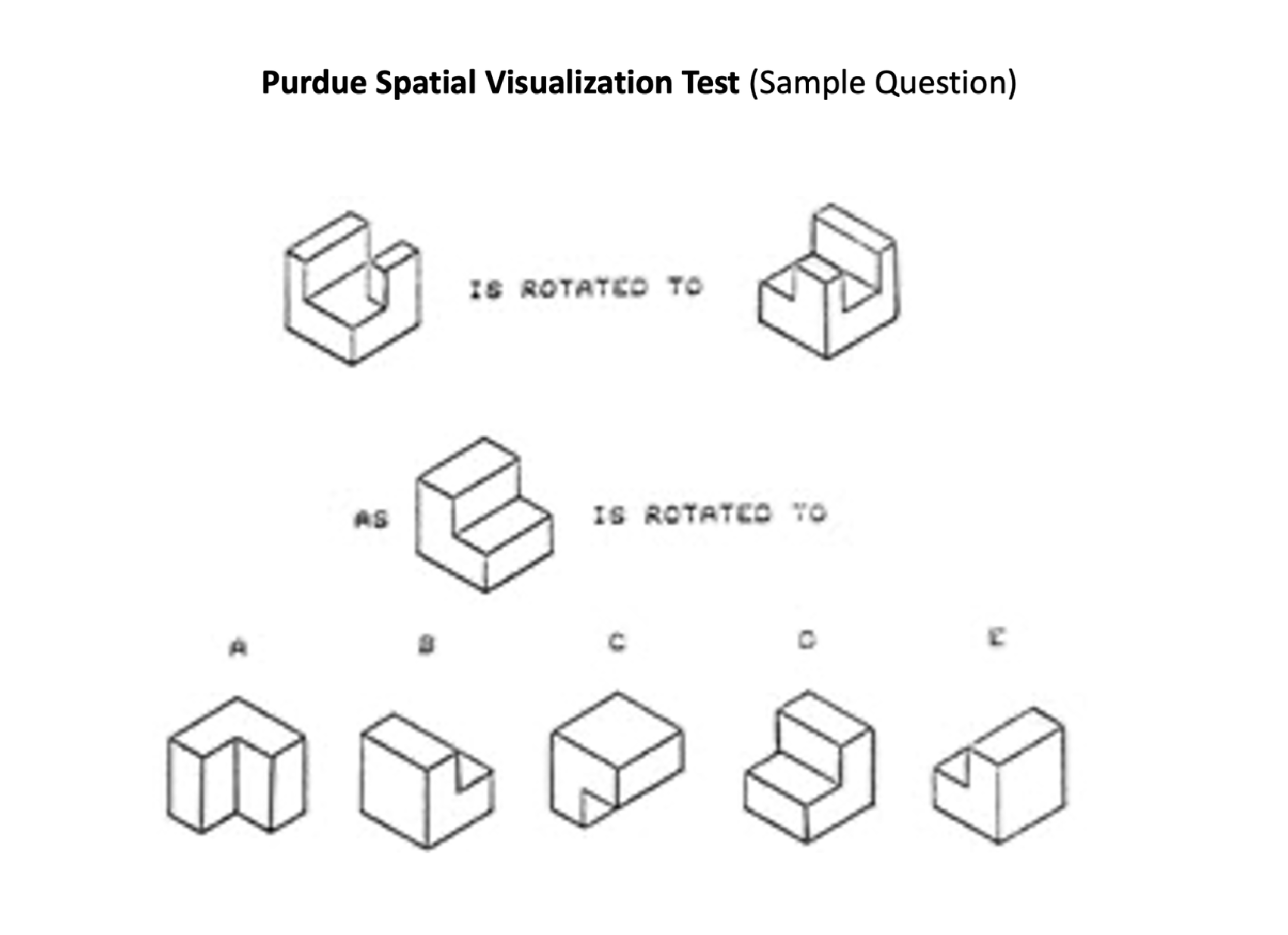
Yet spatial-temporal reasoning is not taught explicitly anywhere in a typical K-12 curriculum. However, students who’ve played ST Math will find this type of reasoning uncannily familiar and be better prepared for academic and future success.
I invite you to learn more about our remarkable, schema-building tool and to learn how you can join MIND’s mission to ensure that all students are mathematically equipped to solve the world’s most challenging problems.
Nigel Nisbet is Vice President, Content Creation, at MIND Research Institute. He devotes his time to reaching into the structure and beauty of mathematics and finding ways to build engaging, interactive and completely visual games that teach all students how math really works.
.png)
Comment