
The jobs of the future are in STEM. Just think of the most innovative companies in the world. Many are powered by scientists, technologists, engineers, and mathematicians. And according to the US Department of Labor and Statistics, the number of STEM careers is projected to grow by 8% by 2029.
STEM is more than an acronym. It's a mindset—an agile way of thinking that embraces challenges and activates several areas of the brain to solve problems. Developing the skills essential for future STEM career success starts with a solid understanding of mathematics. However, the educators we speak with time and time again tell us that conventional algorithmic approaches are leaving students behind. In a report from the American Psychological Association, it's said that having a deep conceptual understanding of math creates the problem-solving foundation that all areas of STEM are built on, and early math skills are powerful predictors of later learning.
So how can we make math learning more intuitive and accessible for students? By teaching math the way the brain learns!
To illustrate just how our brain learns new things, draw on your existing schema of a laboratory. Our thoughts are like small experiments: reacting to stimuli, predicting an outcome, and analyzing results every time new information arises.
Neuroscientists define this process as the perception-action cycle: the feedback loop helping us build an understanding of how the world works. Knowledge like this that gets encoded in our brain through the perception-action cycle is extremely powerful and easy to retrieve. That’s what makes the perception-action cycle so valuable: it is the default way we make sense of the world around us and decide how to live in this world.
ST Math is a game-based instructional math program developed from neuroscience research at the University of California, Irvine. It embeds spatial-temporal reasoning into the learning process as students manipulate visual models to solve problems. This highly innovative approach has been shown by multiple large-scale research studies to have statistically significant positive outcomes for students on state standardized mathematics assessments and to increase students’ self-efficacy for mathematics.

In addition to teaching the “M in STEM” for students from PreK-8 in an innovative way that engages all students in a journey of productive struggle, ST Math also creates problem solvers and critical thinkers: attributes that are at the heart of a STEM mindset. It does this through the engineering design process, “I think, I try, I learn” (predict, test, observe) that's at the center of the learning students do every time they tackle a puzzle in ST Math. In ST Math, students will solve around 3,000 puzzles to progress through a single grade level.
Spatial reasoning is central to the learning in every ST Math game, but there is a series of games that effectively engage and build students’ “pure” spatial-temporal reasoning skills. These are some of the skills most correlated to young students’ future college attendance (Duncan et al., 2013). Here are some of the best examples of ST Math puzzles that specifically grow spatial-temporal skills.
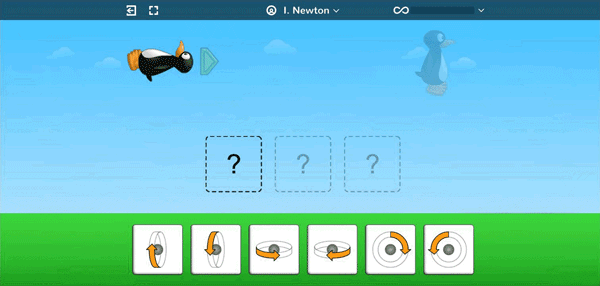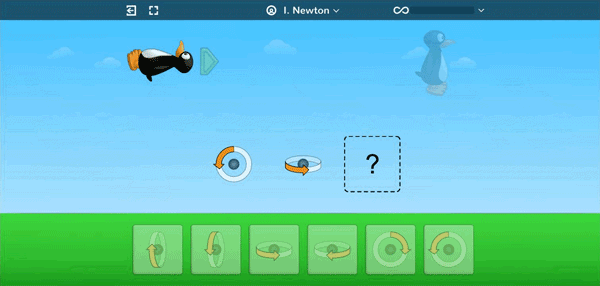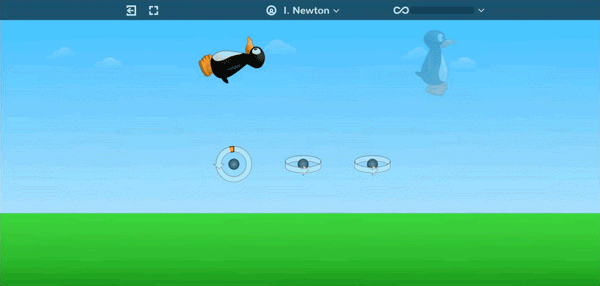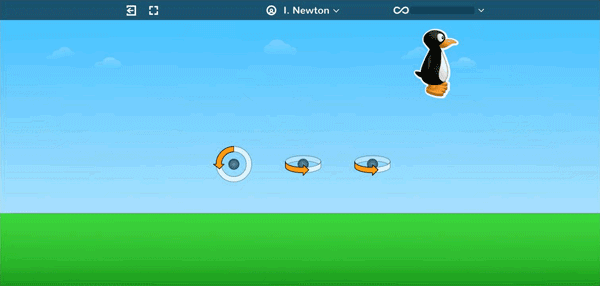
Students as early as Kindergarten learn to apply sequences of rotations in order to help JiJi orient to be upright and walk across the screen.
At the higher levels of the game, students must plan and test a sequence of multiple moves in order to be successful. The immediate formative feedback helps them build spatial-reasoning skills and schema.
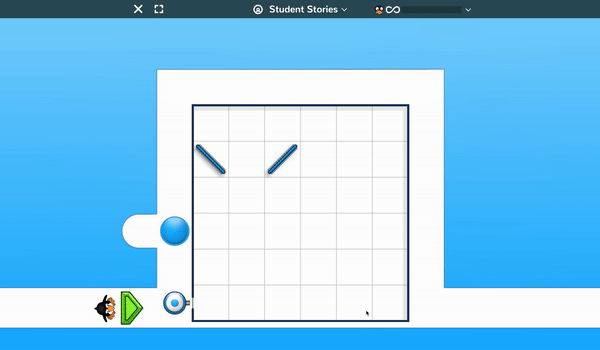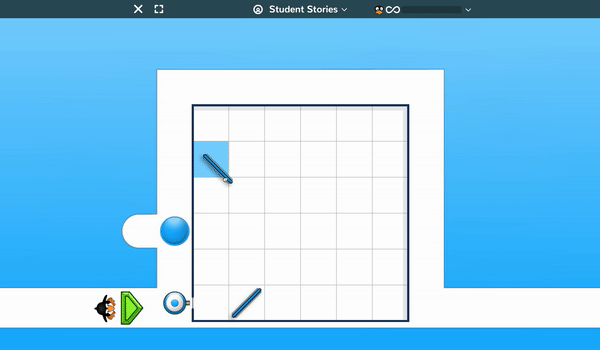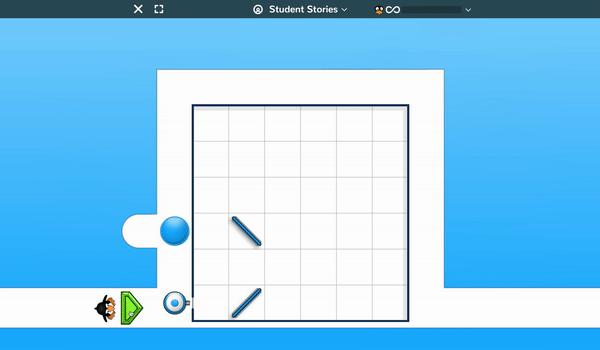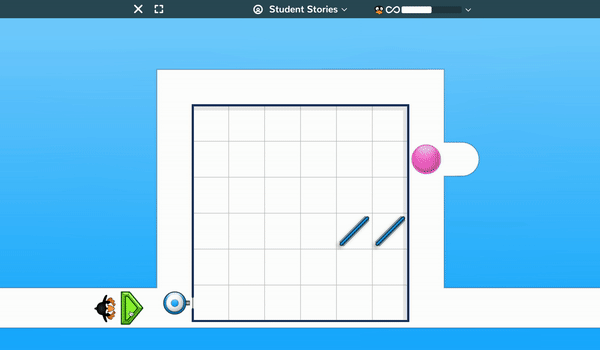
Students must drag and position laser relays and mirrors on a grid so that the balls blocking JiJi are pushed aside enabling the penguin to walk around the path.
Early levels have only one or two objects to move into position so students can readily learn how the game operates, but at higher levels (which are extremely challenging for students and adults) there are a large number of objects to move and a need for some real “out-of-the-box” thinking in order to be successful.
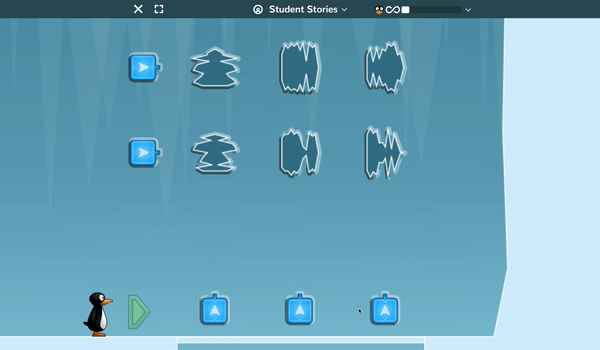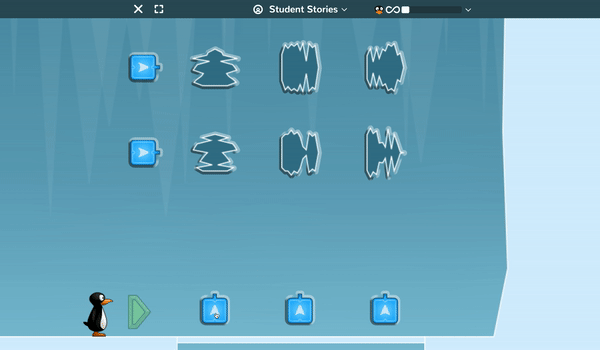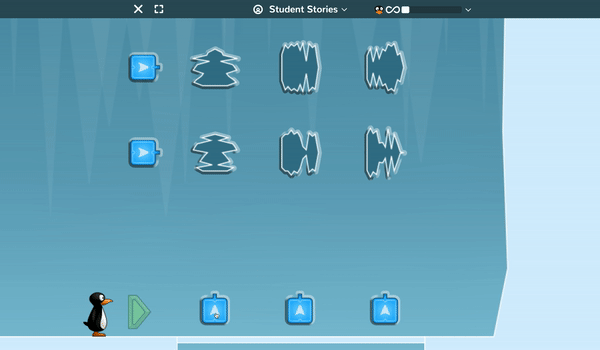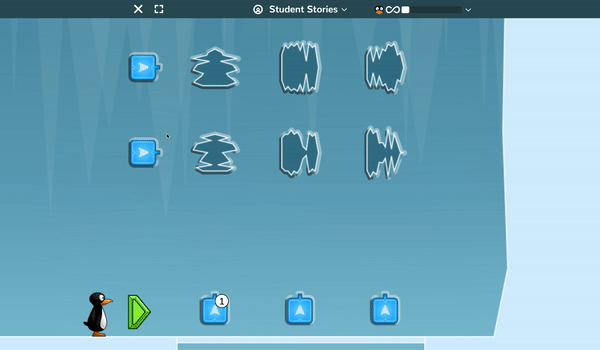
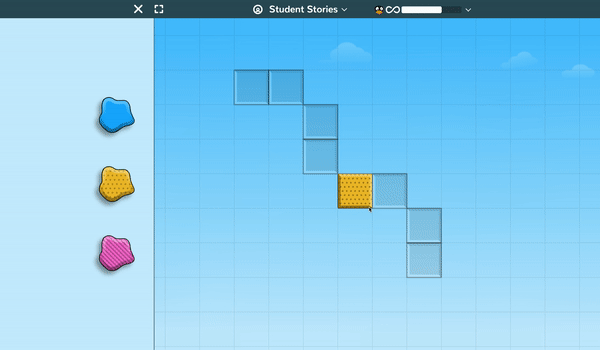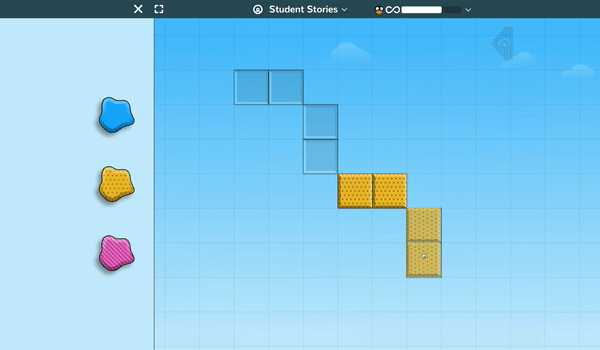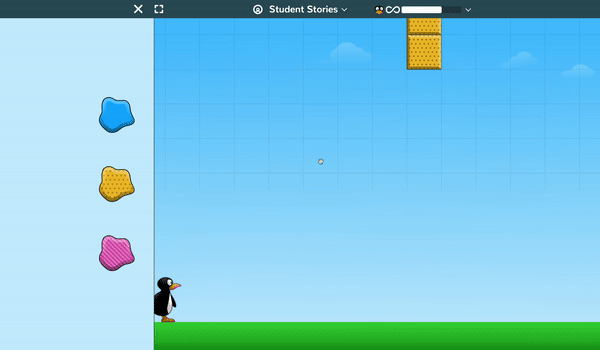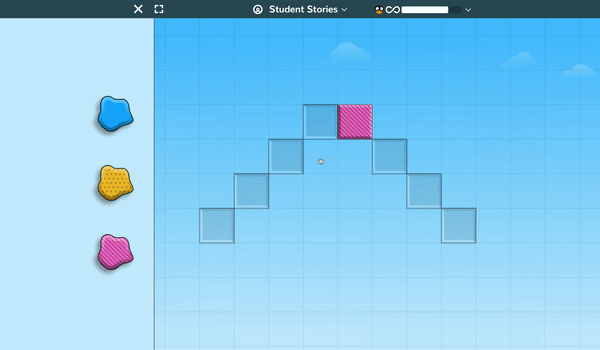
Lines of symmetry and sequencing are the critical factors students must understand to help JiJi progress through the ice caves. In this game, the lasers will only split the ice boulders along their lines of symmetry and students must set the order that the lasers fire in so that they destroy every boulder in the cave.
Again, early levels allow students to understand the game mechanics before later levels require students to correctly sequence up to 12 lasers to clear 16 different ice boulders.
This game is based on knot theory, the subject of a neurological research paper on the identification of genius (Peterson et al., 2004), and referenced as a tool to understand DNA structure (Bodner & Shaw, 2004). Students must determine how to unfold the squares in any of eight directions to correctly fill the complete grid structure. Be warned that later levels are only solvable if you employ the color change buttons in the middle of the unfolding process. Some puzzles can take upwards of 20-30 minutes of deep critical thinking to solve.
In addition to these “pure” spatial-temporal reasoning games, ST Math also has a sequence of games, spanning multiple grade levels, that focus on building students’ abilities and understanding of data visualization—a need in STEM education spanning multiple disciplines.
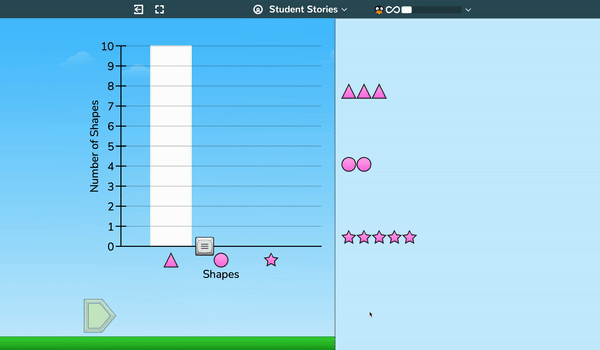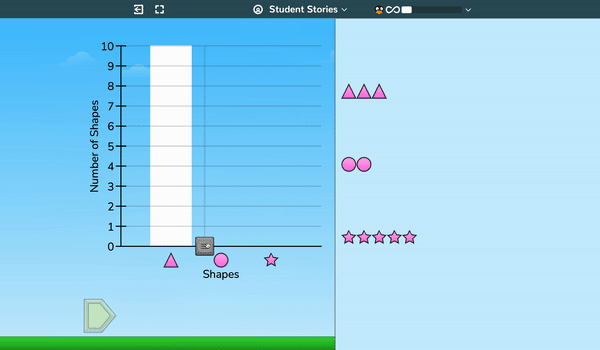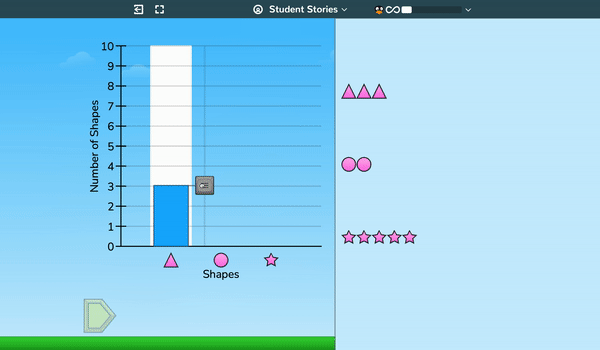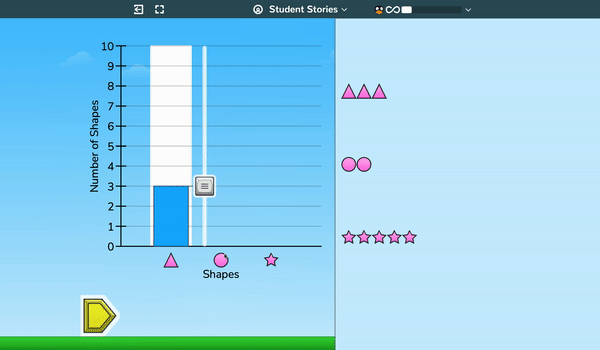
As early as second grade, and building on work with attributes of objects from Kindergarten and grade 1, students use a bar graph tool to model groups of objects—sometimes drawing the graph as shown and sometimes creating objects based on a given graph.
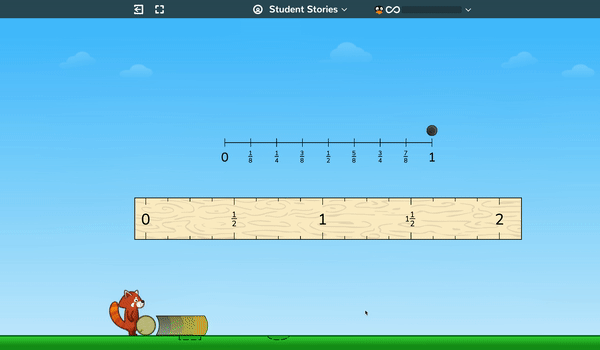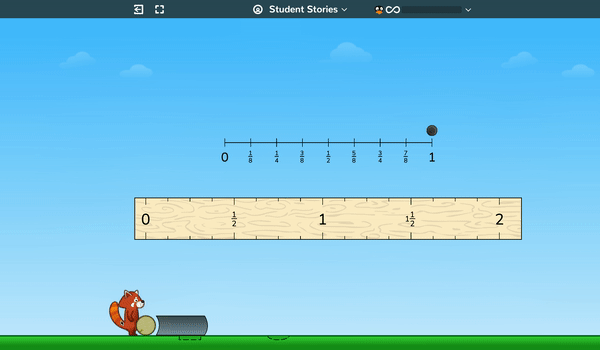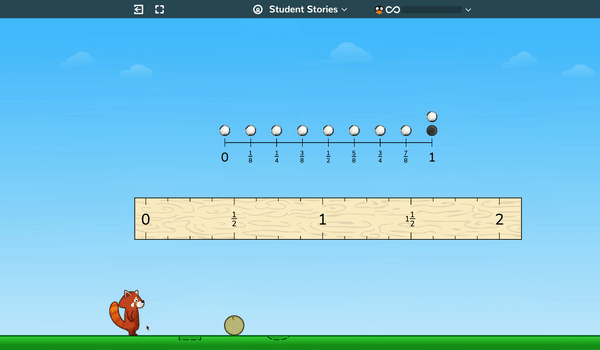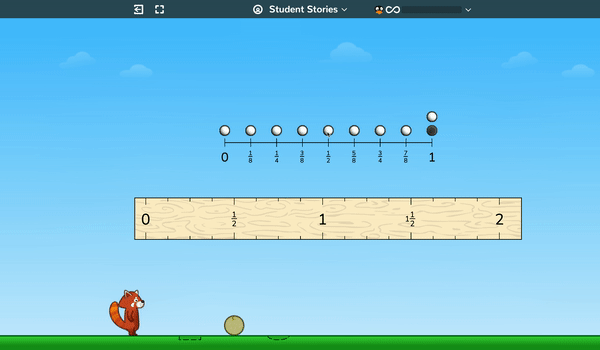
In upper elementary, students build and analyze line plots—initially by generating all the points themselves—by “kicking” a ball a variety of distances and then plotting those distances on a line graph. Students will analyze these plots, discovering useful ways of classifying, sorting, and describing the data, like mean, median, mode, range, and so on.

By middle school, this analysis grows even more advanced. Here, for example, students need to determine how a line plot distribution needs to be modified in order for the mean to be greater than the median. In this case, by skewing the data in a positive direction, the increased spread of the larger values causes the mean to increase while the median remains the same.
Note: while the ST Math games mentioned here have a far-reaching impact on developing STEM thinking for all students well beyond just meeting mathematical standards, it is important to note that by far, the most research-driven and effective implementations of ST Math occur when students are using the program for at least 90 minutes per week in a coordinated way in conjunction with their core math program. The optimal use case of ST Math requires that a math teacher be part of the implementation, monitoring student progress and using the data provided by the ST Math reporting system to ensure all students are meeting learning goals.
Students who sharpen their spatial-temporal reasoning abilities now will be set up for success in the rapidly expanding STEM economy. As mathematics establishes the foundation for all STEM fields, the traditional instructional methods we’ve become accustomed to simply won’t cut it anymore. By encouraging students to lean into their curiosity, test ideas, and learn from their mistakes, we will open up new neural pathways for discovery that encourage innovation.
Want to try your hand at more ST Math puzzles? Sample some free grade-level games and start changing the way your students see math.

Nigel Nisbet is the Vice President of Content Creation at MIND Education, a non-profit organization dedicated to equipping all students to solve the world's most challenging problems. He is also the author of the E-book “I think, I try, I learn” and presenter of the TEDx talk “The Geometry of Chocolate."
Comment