
What makes understanding fractions so challenging? A study from the University of Cambridge suggests that how fractions are written is to blame. Both adults and students have more difficulty processing the multiple numbers involved in one fraction.
Look at the fraction ¼.
A fraction is a single value. But we represent a fraction using multiple numbers (1, 4).
In this example, students must identify the numbers one (1) and four (4), and the relationship between the numbers. That’s a lot for our brains to process, especially when we are unfamiliar with fractions.
This is one reason why emphasizing that a fraction is a value in and of itself is very important to developing that conceptual understanding of fractions. A solid understanding (or schema) for fractions can allow us to automatically manipulate fractions without investing precious brain power every time a fraction is encountered.
Here are some tools and approaches educators might use to build this understanding:
Conceptually driven, the ST Math instructional program enables students to build a deep understanding of fractions as a number before introducing the symbols. Let’s take a look at the sequence of the JiJi Cycle games in the program to understand how.
Students are first introduced to JiJi Cycle in grade three. In these first puzzles, students explore the relationship between two common ways to visualize fractions: fraction pies and the number line.
In this spatial temporal model, students estimate how far a set of fraction wedges will roll JiJi the penguin onto the number line.
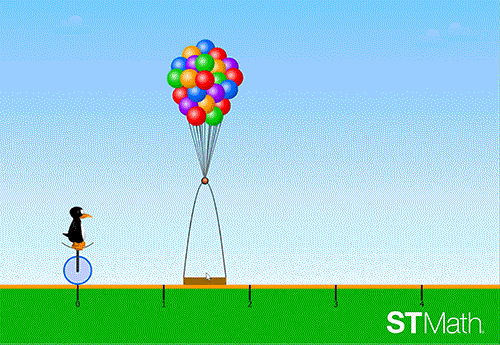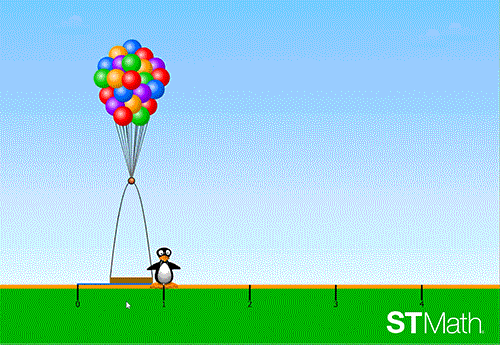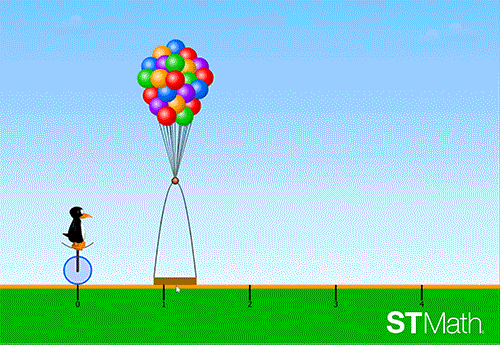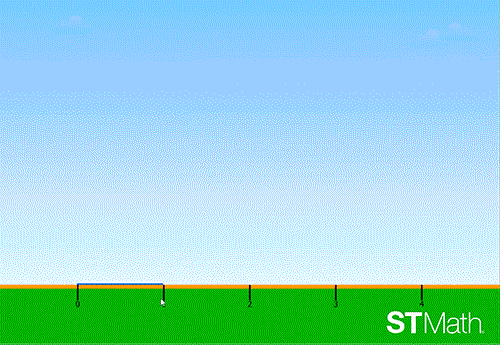
Students move the basket to the point on the number line to estimate the fraction on JiJi’s cycle.
By adjusting the basket’s position on the number line, students visualize their answer. When they submit their answer, the fraction wedges animate to equate to the exact spot on the number line. A full circle (one whole) is the number one on the number line.
When the wheel is done unfurling, JiJi is dropped on the ground. Where JiJi ends up on the number line is the location of the fraction. This informative feedback shows students why their answer is correct or incorrect and how to adjust their thinking for the next puzzle.
If JiJi is dropped where the basket was positioned by the student, both JiJi and the basket get lifted into the sky. The feedback is positive and the student moves onto the next puzzle.
If the basket is not where JiJi gets dropped off, the basket gets lifted into the sky without JiJi. JiJi returns to the beginning of the puzzle and students must try again.
Students can try the puzzle over and over again until they have mastered the concept. Just like in video games, the consequences for failure are low, encouraging students to learn from their mistakes and develop perseverance.
When the mathematical symbols are introduced, students are primed to see ¼ as a single position on the number line, a portion of a whole circle, and finally, a relationship between the numbers 1 and 4.
Play a select series of the JiJi Cycle puzzles on our website for free:
As the levels progress, new elements are added to the game. For example, this level has multiple fraction pieces.

Students still choose where to place the basket. This time, when a wheel is done unfurling, the next wheel drops down and begins. JiJi is dropped on the ground when the last wheel unfurls.
At another level, students encounter a different colored fraction piece. What do you think the red fraction represents?
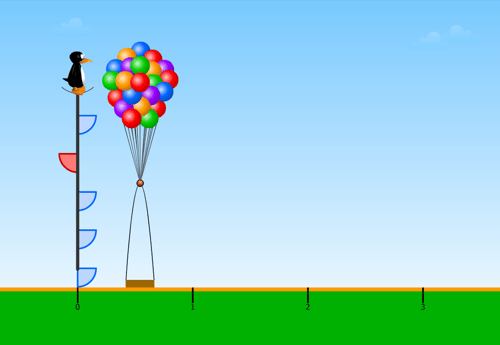
Many students start this puzzle by adding all fractions, just like previous levels. Observant students might notice the different color. As they try their first solution, the informative feedback shows the red line unfurling to the left, the opposite direction of the blue line. The feedback shows how the game (and the math) works.

Just like the first levels, the levels progress to include mathematical symbols after students have mastered working in the spatial temporal models.
The game continues in later grades, to include concepts such as adding and subtracting unlike denominators. How the levels are scaffolded throughout the grade levels shows how math concepts are connected. Instead of learning concepts as separate formulas and sets of rules, students experience and build upon their understanding (or schema) to see how mathematical concepts are connected.
Experience the spatial temporal models and immediate informative feedback for yourself by trying a free sequence of the JiJi Cycle games on our website. You can set up a lesson incorporating this spatial temporal model yourself, or follow our Puzzle Talk lesson plan to engage students in mathematical discourse around fractions.

Calli Wright was the Marketing Manager at MIND Research Institute. She loves playing and designing board games, which she often talks about on twitter @CalliWrights.
Comment