
People have very different responses to fractions. Some just want to know the steps to follow. Others understand fractions intuitively but get confused when asked to write things down or solve word problems. Then there are those who simply run in fear as soon as the word “fraction” is mentioned!
Wherever you fall in this spectrum, the following are a few tips for you to help your children avoid some common pitfalls when learning about fractions.
A lot has been written about the fallacy that there is some sort of selective genetic code for mathematics. True, some people have an aptitude for math. However, when it comes to the math content being taught in K-12 (including fractions), pretty much everyone can learn to do it.
Many schools and even some entire countries have almost all of their kids scoring proficient in math. So, brush up on your skills, do your best to muster up a positive attitude and be a good example for your child.
Research shows your kids will learn your attitude along with any mathematics you help them with.
“Numerators” and “denominators” are big fancy words. They can be a challenge for young kids to say, much less understand.
With all of the content teachers need to cover, there often is not enough time to thoroughly discuss the meaning of these terms. We just jump straight into learning procedures for equivalent fractions, fraction addition, common denominators, etc., before kids have developed a solid concept of numerator and denominator.
This lack of understanding may not show up right away. In fact, you can happily add fractions involving mixed numbers and uncommon denominators by memorizing the procedures — and still have no idea what a denominator is. But memorization is not enough and one day, you will hit a wall.
So, what is a denominator? It’s the number on the bottom, right? Pass… and fail.
If we use this answer with our kids, we are really missing the boat. Yes, the numerator is written on top and the denominator is written on the bottom. No, that doesn’t tell you what they actually are.
Keep in mind that the schema, or understanding, of denominators builds up over time. When you’re helping your child with math homework, it’s a good idea to take the time to check in periodically about what the denominator means in a given situation. It can refer to equal parts of a whole (hint: ask “what is the whole?”), or parts of a group. Later on it might be part of a rate, or represent division.
At the very beginning stages of understanding fractions, try to make sure your kids understand the basic denominators (halves, thirds, fourths, etc.) are similar to units (miles, pounds, planes, cars, etc.) in that they tell you what type of fraction we’re talking about.
This will help clarify why they can’t just add fractions with different denominators. Kids know that 3+2=5. But, 3 planes + 2 cars does not equal 5 planes, or 5 cars, or 5 flying cars. In this same way 3 fourths plus 2 halves doesn’t equal 5 fourths or 5 halves.
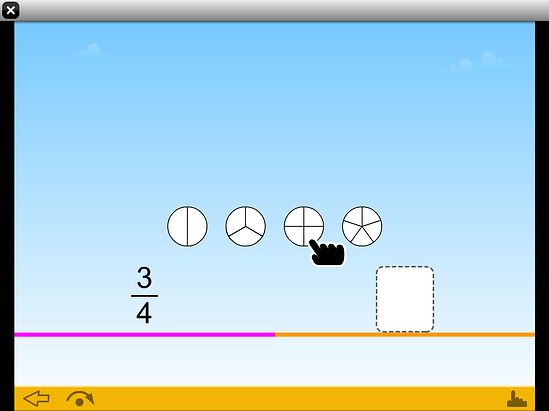
In this example in ST Math, students make the connection between the denominator and the number of parts.
Numerators, on the other hand, tell us how many of these “fourths” (for example) we are referring to. Before jumping into procedures, check in with your kids about the meaning of numerators in the same way you can with denominators.
If their understanding seems a little cloudy, talk about what a 1 in the same position would mean. For example, if the fraction 9/4 isn’t making sense to your child, talk about the meaning of 1/4, and then make a connection to 9/4 from there (maybe stopping along the way to discuss 4/4).
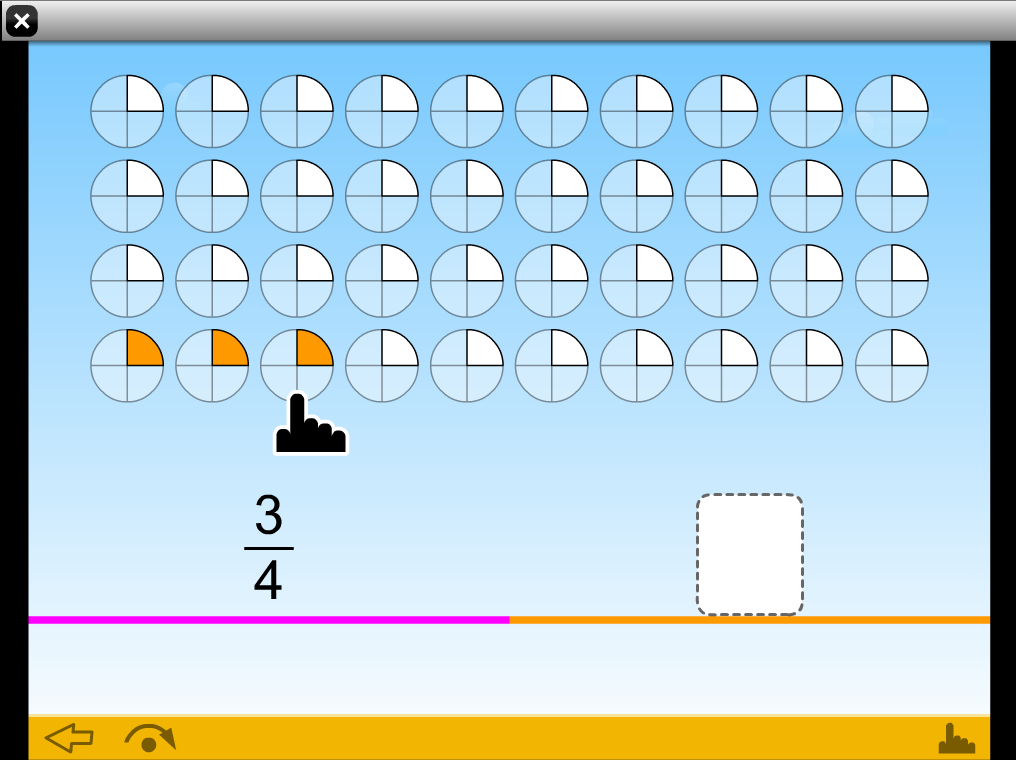
In the next section, the student identifies how many of these parts the numerator represents.
Everyone loves pizza, especially kids. And when we want to help our kids understand fractions, we like to say, “Imagine we’re talking about pizza…” However, kids have often seen this model — and sometimes only this model — at school. In fact, they’re often good at this model.
It’s when fractions have to be applied to something else that they get into trouble.
So, I suggest offering multiple models, such as drawing number lines or making fraction strips.
Throw in some examples related to money (quarters, cents) or recipes (¼ cup, ½ teaspoon) and now you’re, well… cooking!
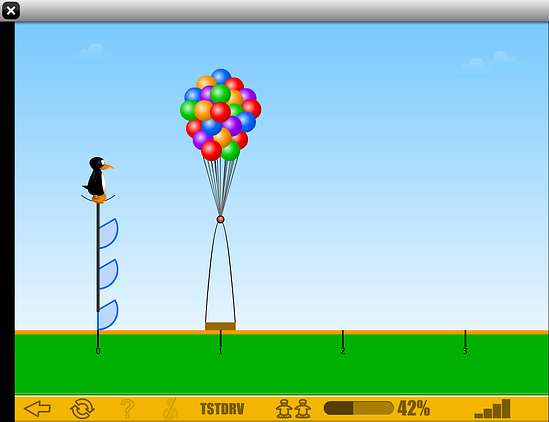
Example of an ST Math number line puzzle
The reality is that fractions will eventually tie in to so many things: rates, ratios, percentages, decimals, money, time, etc. The more examples and connections we can make for our kids, the better.
If you’re filling your gas tank, teach your kids to divide miles driven by gallons pumped to check your gas mileage.
If you’re going on a trip, help your kids figure out how long it would take to arrive at your destination if you drove 55, 60 or 100 mph.
This can be a little confusing. We were just talking about numerators and denominators, and our kids are learning lots of procedures where they cross-multiply or in some way treat the “number on top” and the “number on the bottom” as separate entities.
However, it is important to remember that 11/16 is a number, too. And I mean that whole thing: The one, one, slash, one and six, altogether, is actually a number unto itself. Sometimes our kids never really make this connection.
The same kids who can add and multiply fractions using the procedures often can’t find a single fraction on a number line because they’re not yet seeing the whole symbol as a single number.
Understanding “Which fraction is bigger?” problems also become a lot less confusing when kids aren’t comparing individual numerators and denominators, but seeing the fractions as numbers.
Whatever potential fraction pitfalls your kids may face, the important thing to remember is that learning fractions shouldn’t be mysterious. Fractions are simple logical symbols and any procedures students memorize should make sense to them.
If you take the time to slow down and demystify things, your kids will benefit, and your efforts will help end the cycle of fraction frustration in this country.
Get more tips on how you can help your child with math at home:

Eric Sbar is Regional Vice President of West Partnerships for MIND Research Institute. He is a musician and educator, and enjoys connecting with math through nature while hiking, camping and sailing.
Comment