During this challenging and uncertain time, we’re being asked to take care of and be responsible for our communities, which means slowing down. While this change of pace limits us from a lot of our usual activities, one thing we can still do is bake! If you’re looking for things to do as a family at home, may I suggest baking together and exploring the many math questions that arise along the way. It doesn’t have to be Pi Day to eat pie.
Another Pi Day, another pie! Going on my sixth year of this personal tradition, I was grappling for a theme or source of inspiration to keep it fresh. Each year is another opportunity to see what insights a pie can offer mathematically and creatively. This year, I reached for a pun, so may I present to you, the Pie-thagorean Pie!
To make this pie, I was inspired by lokokitchen and found that any curd pie or tart is a good base to support the fruit tile design. (Her puns are also 💯!) I sourced from a couple of recipes - this one for the crust, and this one for the curd, substituting the lemon with grapefruit and ginger since that’s what I had on hand and I was feeling adventurous.
For the fruit tiles, I needed something that would be easy to make square tiles out of, has a uniform texture, and would be a good contrasting color from my curd, so I went with dragonfruit. (Mangos or melons are also good options.) But really, this idea of a curd pie with fruit tiles is incredibly flexible for whatever ingredients you have on hand!
While the connection between pi and Pythagoras is very loose, this pie is a fun way to connect them and a great starting point for mathematical inquiry for students of all ages and ability levels!
Spend some time researching Pythagoras. Math is so much more than equations and numbers. The history of math is part of our human story and truly fascinating! The Pythagoreans were a cult-like following of Pythagoras and studied math to the point of mysticism. Believing that numbers ruled the universe, they assigned numeric values to virtually everything.
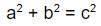The Pythagorean Theorem is an 8th grade standard, so everyone eventually learns it, but it’s so much more than memorizing this formula.
Challenge your students to inquire why this relationship exists or look deeper into other applications of this formula, because it’s not trivial. It took a whole cult deeply studying numbers and math in the physical and spiritual world to discover it! One can see why the Pythagoreans were mystified by math because this relationship is true for all right triangles! (Where a and b are the legs of the triangle, and c is the hypotenuse.)
Although the Pythagoreans are most known for the Pythagorean Theorem, I’d venture to say their greatest contribution to math is the discovery of irrational numbers. Up until this time, it was thought that all numbers were “known” and could be expressed and created by place value and ratios (i.e. rational numbers).
But, for example, looking at a right triangle with unit sides,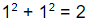 
, means the hypotenuse is √2, which defied all their former rules and understanding of numbers. These irrational numbers were to be kept a secret and speaking of their existence was punishable by death.
The Pythagoreans discovered the existence of irrational numbers around 500 BCE. While the notion of pi was known from the time of the ancient Babylonians (~1900 BCE), it wasn’t proved to be an irrational number until the 1760s.
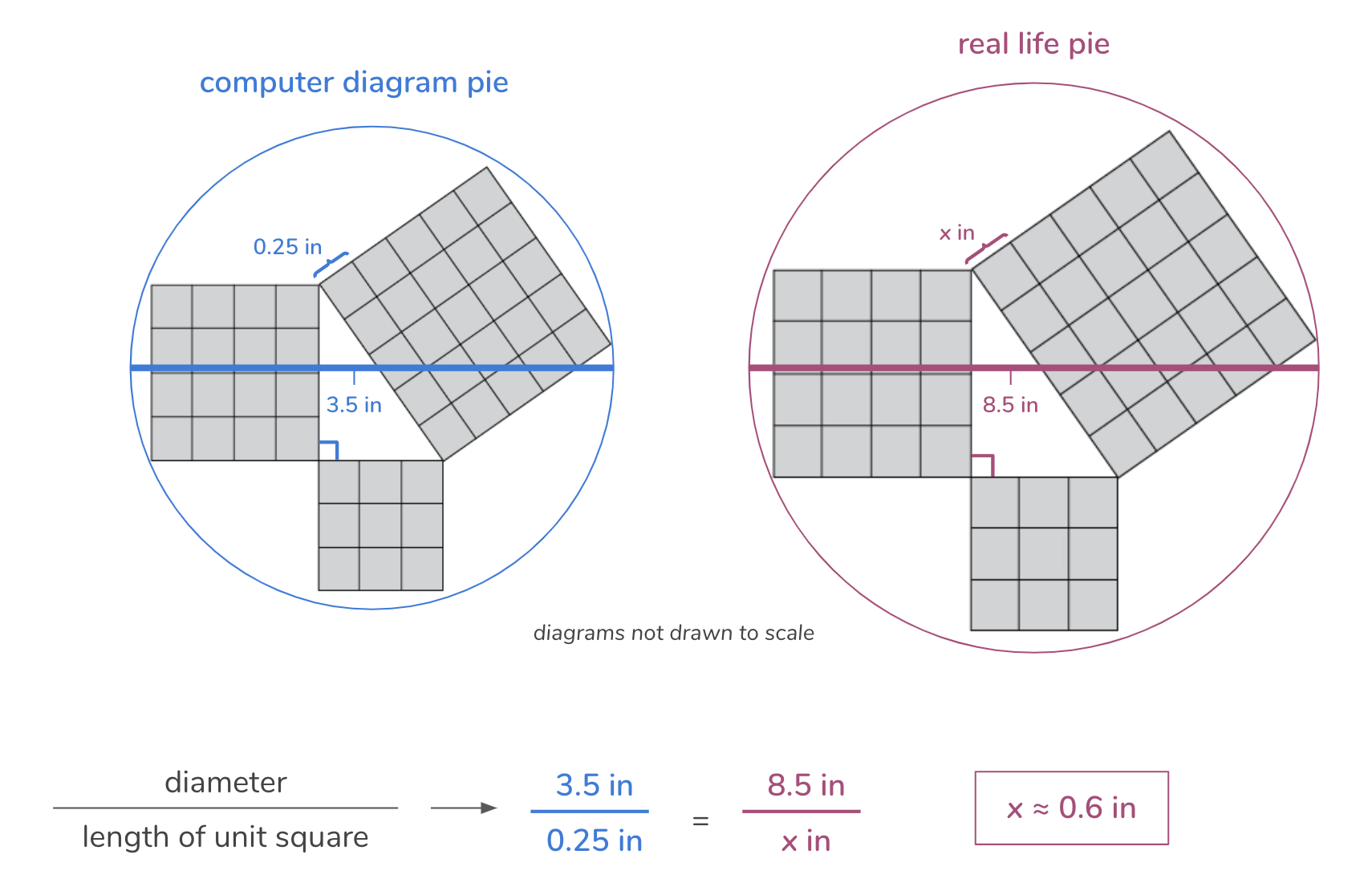
I knew I wanted to use this diagram of the Pythagorean Theorem, so I had to use proportional reasoning to figure out the scale of my pie design. I made a scale model on my computer of what I wanted for my real life pie. Depending on the design you choose, the size of your pie, and the scale of your model, your measurements may turn out differently. But the power and properties of proportions will hold!
I used dragonfruit for my fruit tiles. It’s not an everyday fruit for most of us in the US, so this could be a good opportunity to expose students to new things! I also think dragonfruit offers an opportunity for a lesson in data collection and analysis.
The Pythagoreans were the first to identify the difference between even and odd numbers. You could use the fruit tiles as counters to create odd and even amounts. (Each time you eat a tile, notice how it changes from even to odd to even…) You could also make a design based on odd and even numbers.
The Pythagoreans were diligent students of geometry and believed that the circle was the parent of all shapes. Using overlapping circles and straight lines, they could create triangles, from which they could construct more shapes. This Pie-thagorean Pie could be a geometric study and you could create designs based off of these other Pythagorean shapes.
What I love about creating pies for Pi Day is that the pie is a blank canvas for whichever math question you want to explore. Those math questions lead to even more questions, discoveries, and lessons. It invites you to make connections across ideas and be creative with the ingredients you have on hand. At the end of it all, you also have a tasty pie to eat and share!
Let us know what you came up with, what you learned, any insights you had.
Take care of each other, be kind, be gentle, be sweet.
Nina Wu is an Educational Game Designer at MIND Research Institute. She enjoys finding the math in her daily hobbies, including dance and art.
.png)
Comment