A few years ago, while I was still a relatively inexperienced classroom teacher and long before the 2020 education challenges of dealing with the COVID Slide, I began a new school year full of optimism and excitement only to find that 75% of my 9th grade Algebra students were unable to correctly answer a 5th grade fractions question that I had mistakenly assumed would be pretty easy...
Most of the students chose C, or D, either adding across the top, or the bottom.
And suddenly I had a huge dilemma, the same dilemma facing virtually all teachers, schools, and districts as they start school - in some fashion - this fall: how do you remedy the fact that a significant number of students, but not necessarily all, have large learning gaps in the math they should have previously learned? You can’t really put all the students back in 4th grade!
I took what for me seemed like the most logical path, I gave a diagnostic assessment, provided the relevant online remediation materials for the students as needed, and tried to do some reteaching of the “big gaps” that were shared by a large number of the students (like fractions, for example). Unfortunately, this approach was a complete and utter failure! The gaps persisted, and trying to teach Algebra with such an unstable foundation was practically impossible.
It would be easy in this situation to blame everybody; the students “Well they didn’t try hard enough” or “They were just too far behind”, or myself “You’re a new teacher, you don’t really know what you’re doing”, or the materials “They were too text based, the kids just couldn’t learn effectively from them.” Certainly I did a mixture of all of those at the time.
But the real culprit here is much bigger than all of these. The “Theory of Action” upon which I based this entire remedial strategy is fundamentally flawed, and my fear is that this same mistake will be repeated at a vast scale as districts try and grapple with the educational challenge posed by the impact of COVID-19.
Let’s call this flawed theory of action the “Swiss Cheese Model of Learning.” It’s the idea that we can “diagnose” students with a surgical assessment, find the gaps in their learning, and then fill those gaps by providing materials that address them. It feels so compelling and so logical, and yet it does not represent how the brain learns, especially a complex interconnected topic like fractions.
We learn by building schemas, interconnected webs of neural networks, that we use to solve problems and make sense of the world around us. When the world works the way we expect it to, and we are able to solve the problems we are confronted with, the schema we have are reinforced and made stronger, but when something happens in a way that doesn’t make sense, or our efforts to solve a problem result in failure, we extend our schema or build new ones.
In the case of my students trying to solve the fractions problem, they needed a deep conceptual understanding of the problem: ⅞ is a number that is close to 1, as is 12/13, put them together and you have something that is approximately 2. Sadly, they had a mishmash of poorly understood fraction addition procedures, not a genuine fractions schema, and all my assessment and remediation materials did was add more layers to their confusion.
The problem is, you can’t build schema by “telling”. How many times have we heard the adage, “I told them but they didn’t learn it”? A good example of this is humor. 
Jokes often work by activating one branch of a schema - like in this example, the word “improper” can mean “that’s not appropriate behavior” - and then with a punchline or visual, it switches to another branch of the connected schema - in this case “improper” as a type of fraction. If you have both of these branches of this schema, we find this "schema switching" amusing, we laugh! However, if you don’t have the relevant schema, no amount of telling you why the joke is funny is going to recreate the moment of laughter. You can’t build schema by telling.
Unfortunately for my students, it would seem the only way to really address their insufficient fractions schema is to go back to 4th grade and have them spend the time building fractions models and develop the deep conceptual understanding they need.
Let’s look at a different way to solve this problem, one used by ST Math, and one that has years of research and proven results behind it. Mastery-Based Embedded Assessment tackles the challenge of the COVID Slide head on, and solves it during the learning process in three ways.
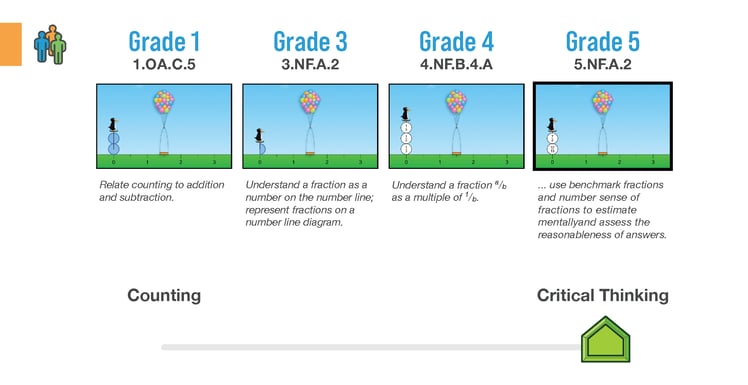ST Math groups content into game-based learning objectives, where students solve sequences of puzzles to build and attain mastery of a concept. Not only do the puzzles scaffold from being highly visual and then gradually introduce the relevant symbolic notation, but they also start from below grade level standards and build in a “low floor high ceiling” type model so that no matter where students are, ST Math quickly builds the foundation and enables them to tackle the on-grade level mathematics with confidence.
To complete a grade level, students will solve many thousands of math puzzles. In every single one, the student receives immediate formative feedback on their actions and thinking as they try and solve the problem. These are the schema building moments so critical to deep learning. If correct, their existing schema are reinforced, but if not, they immediately see why not in terms of the actions and solutions they attempted, and students extend their schema or start to build new one’s - this is neuroscience in action on an everyday basis in thousands of schools across the US, students are learning by doing, learning by their mistakes.
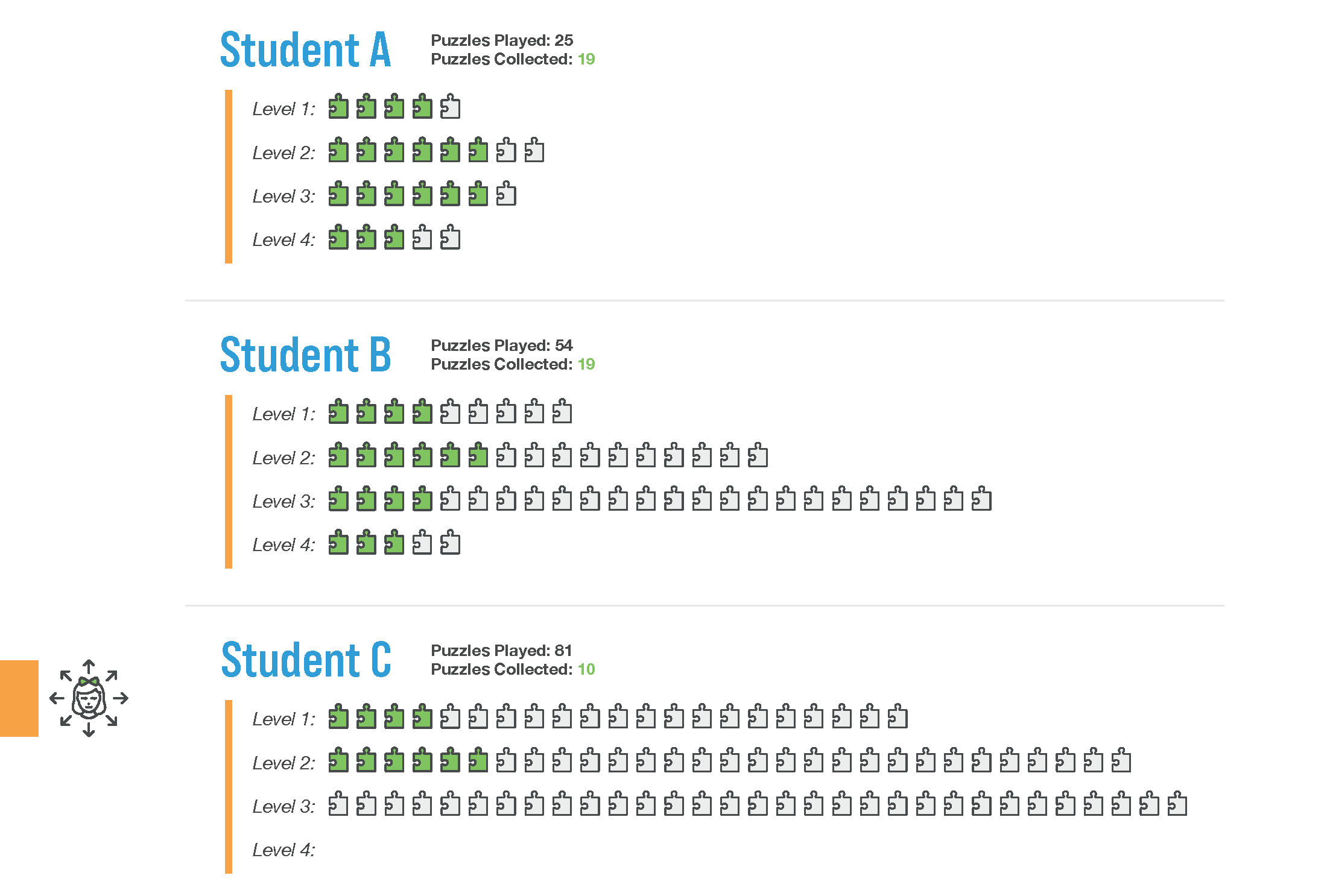Rather than dropping students down from grade level content, ST Math takes students deeper into concepts they are struggling to master, using scaffolding techniques, and randomly generated puzzle sequences. Instead of going backwards to experience success, ST Math surfaces just-in-time supportive material that elevates students to their target grade level. It makes them successful where they should be.
Above we see three hypothetical students, each has mastered a series of levels in ST Math, but the pathway through was very different for each student, and the number of puzzles randomly generated by the system was determined in real time by the embedded assessment inherent in this mastery-based design. In this model, students will get the opportunity to develop conceptual understanding, practice, and apply their learning by working through as many puzzles as needed to achieve 100% mastery of the content.
And the data shows this approach is effective across all student subgroups, which is obviously critically important for schools and districts as they figure out how to provide learning materials that will be effective not only across different practical models of learning, in-person, remote or a mixture of the two, but also learning that will work for the wide variety of learners they serve.
ST Math's visual approach makes the program accessible to all learners. When students of all levels, whether ELL, special education, or gifted, can problem solve without distractions, educators see dramatic increases in achievement.
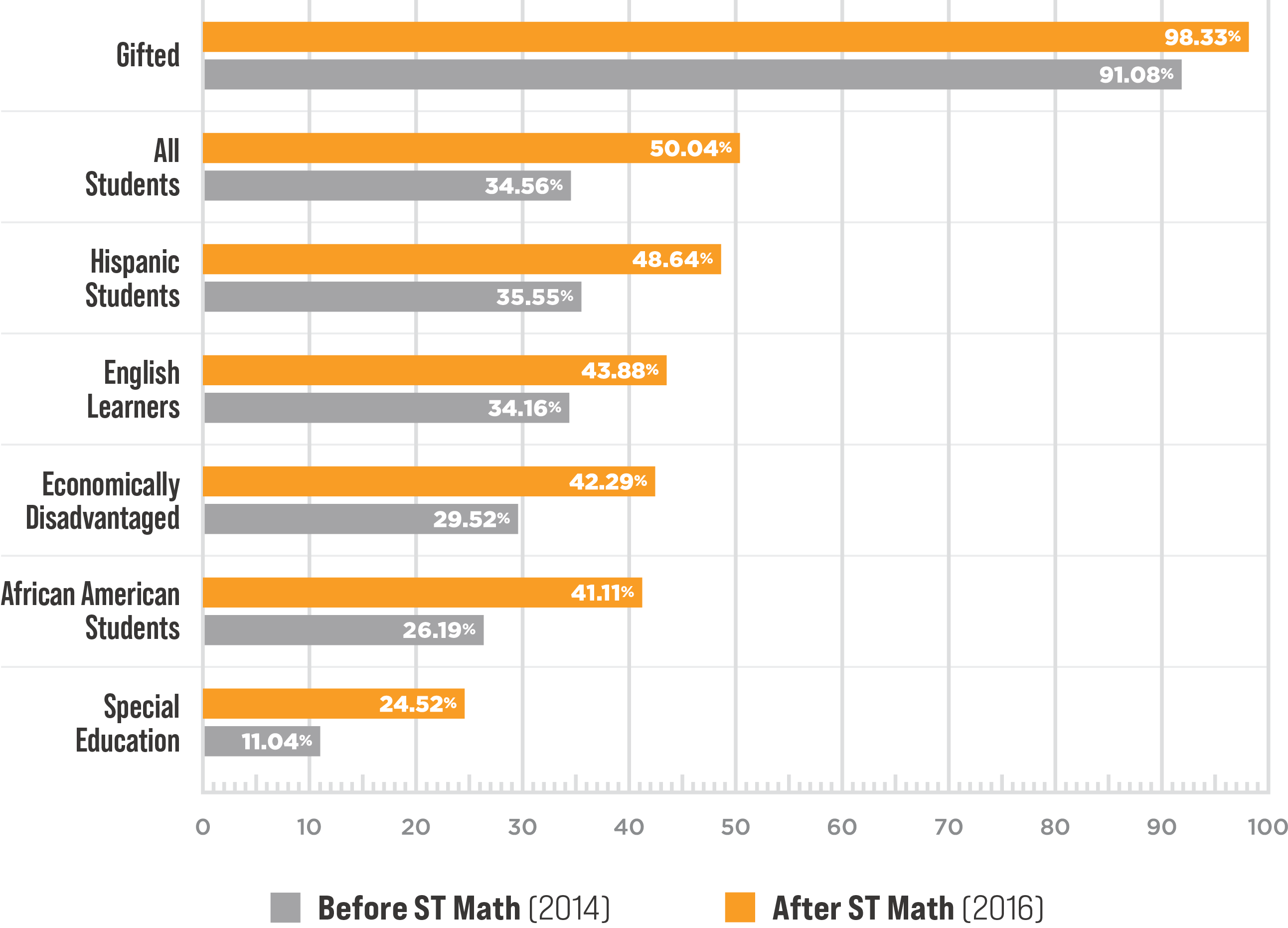
Percent of students meeting or exceeding standards in grades 3-5, 2014 vs 2016.
See full reports below:
All Students | Gifted | ELL | EconDis | Special Education
ST Math is a flexible instructional tool that can fit easily into many different implementations. Whether your students use the program in a computer lab, during designated classroom time, station-rotation, a hybrid learning model, or at home, as long as they’re putting the time in each week, you will see gains in their math achievement.
To learn more about ST Math, how the program is all-new for the 20-21 school year, and to see results from schools and districts across the country, visit stmath.com.
Nigel Nisbet is the Vice President of Content Creation at MIND Education, a non-profit organization dedicated to equipping all students to solve the world's most challenging problems. He is also the author of the E-book “I think, I try, I learn” and presenter of the TEDx talk “The Geometry of Chocolate."
.png)
Comment