
I've blogged about how my classroom experiences taught me that students learn more deeply when I let them apply their prior knowledge to solve problems, before jumping in and teaching them the mathematical procedures.
But, I sometimes hear our ST Math teachers say, “I don't want my students to play this ST Math game yet because I haven't taught this topic in class.” In most cases, that’s putting the cart before the horse. The games can help students build a visual schema for concepts before they are formally taught in class. This gives students opportunities to make sense of the math by using what they already know to solve new problems.
Beginning with visual problem-solving opportunities sets students up to better understand a math lesson because they can connect the new learning to the concept introduced visually. If you've ever seen students' eyes light up when they make those connections on their own, you know the power of this kind of learning! Here are some practices to get you started:
When selecting a visual math problem, consider whether students of all backgrounds and levels can engage with it. Students should understand what is happening in the problem, but the solution (what to do and how to do it) should not be immediately obvious.
Project the problem for the whole class to view together. ST Math teachers can choose from thousands of animated puzzles arranged by grade level and standards-based topics. Each puzzle presents a visual math problem. Project the puzzle in "teacher mode" for this demonstration. (Log in to the ST Math Teacher Resource Site for instructions.)
Ask students to share with a partner three things they notice about the problem. ST Math games present problems without words or instructions, so students need to figure out for themselves what is being asked of them mathematically and how to play the actual game. You can move the cursor over different parts of the puzzle to show things that light up and things that don’t.
Make a couple of intentional mistakes in front of the class and model how to use information learned from those mistakes to inform your next solution. In ST Math "teacher mode," you can examine the animation that follows an answer, which provides students with this kind of informative feedback that visually represents why the solution didn't work.
Allow students to use tools (blocks, legos, whiteboards or simply paper and pencil) to solve the problem. This is the part where you leave it open to students to relate their prior understanding and schemas to the situation. Students bring what the have to the table and strategize, recreate the puzzle and formulate a solution.
To reinforce the power of continually learning from mistakes, identify some students whose solutions didn't work and give them the opportunity talk about why it didn't work. ST Math students respond well when you involve the beloved main character of the games, JiJi the penguin: "What is JiJi asking you to figure out?" You can guide them in watching the animated informative feedback that shows why a solution didn't work.
As students continue to solve the visual problem at their desks, walk around and ask students to share their strategies with you. Select two to three student-generated strategies that move from concrete (using a physical model) to abstract (solving the problem with equations and/or mental arithmetic). Have the students share their strategies and ask the class to compare them. This discussion should help all students advance their mathematical thinking and connect concrete models to abstract procedures and notations.
I recently visited a class of fifth-graders and posed a multi-step, multiple operation problem from an ST Math game, which would eventually be represented symbolically as 2x + 6y = 26. The teacher had not introduced this topic yet and was nervous that his students would not be able to solve the problem. In the end, he was surprised at what we learned about his students by allowing them to make sense of the problem and apply their prior knowledge in solving it.
The task presented through the ST Math game, "Leg Drape Creatures," was to find all the ways you could put 26 shoes on 2-legged ostriches and 6-legged ants. Notice that any student at any level could engage with this problem.
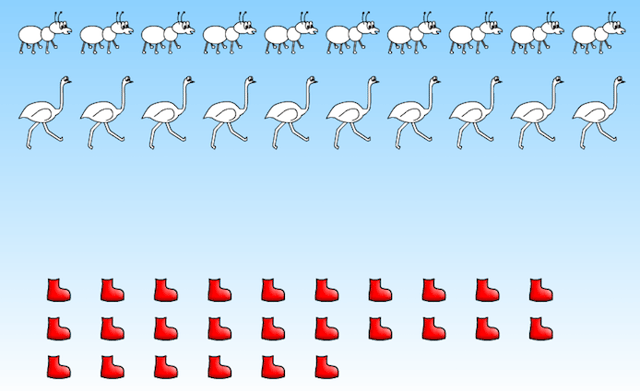
Scene from ST Math game "Leg Drape Creatures"
First, I projected the puzzle for the whole class to see, and after making a couple of intentional mistakes, I knew students understood what the puzzle was asking them to figure out. Students quickly began solving this problem. Through their solutions, the teacher and I gained a deeper understanding of what students knew and were able to apply.
Some students drew out each boot and grouped them in 6s and 2s until no more boots were left. These students often used a concrete, direct modeling method of "guess and check," with little to no organization of the combinations.

Other students applied mental arithmetic and worked systematically to find (and prove they had found) all possible combinations. For example, some students divided 26 by six to find the most ants that could be used and interpreted the remainder (two) as the boots for one ostrich. Then they saw that by taking one ant away, you could put shoes on three ostriches. The pattern eventually allowed these students to stop calculating the shoes for each animal and just continue replacing one ant with three ostriches. Here's the kind of chart they created to organize this pattern:
| Ants | Ostriches |
| 4 | 1 |
| 3 | 4 |
| 2 | 7 |
| 1 | 10 |
Using this chart, they then systematically found all the combinations that worked using an equation like this:
(Ants x 6 shoes) + (Ostriches x 2 shoes) = 26 shoes
(4 x 6) + (1 x 2) = 26
(3 x 6) + (4 x 2) = 26
etc.
The most important point is that these students came up with the math procedures they needed on their own. Here's an example of one student's work and thought process. (Seems like it was easier for this student to call the ostriches "ducks.")
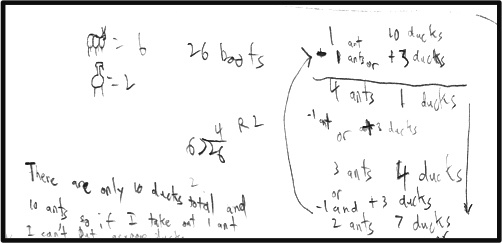
After seeing the wide range of students' solutions, the teacher and I were able to see how best to design the next instructional steps to help all students reach the goal of understanding how symbols can now be used to represent the problem they just solved. Here's one way: Two shoes for each ostrich plus six shoes for each ant equals 26. So 2x + 6y = 26. Find all combinations of ostriches and ants that work in this equation.
Try posing a visual math problem to your class and then come together to explore a new concept with your students, and let us know what you learn!
To find out more about visual problem-based instruction:
More examples of how ST Math paves the way for deeper understanding of math topics:
A version of this article originally posted on Nov. 19, 2014.

Erich Zeller is the Instructional Designer for the Product Team at MIND Research Institute. Follow him on Twitter @ErichZeller1.
Comment