So I would show my students a series of steps (algorithms) shown in the book for the problems in the chapter. This approach was fast and efficient, but not without serious drawbacks. There were always students making the same predictable mistakes over and over again.
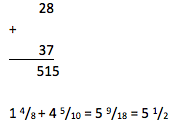
I was astounded that otherwise observant students did not realize that 515 cannot be the sum of two numbers each less than 50 or the missing addend in the given problem be greater than the the sum! Math professor W.W. Sawyer clearly saw how this approach to teaching arithmetic deprived students of their sense making. They lost all quantitative intuition.
I now realize that I was contributing to my students’ lack of mathematical sense-making. In class, I was the source of all mathematical reasoning. They looked to me to give them the steps. And even then, students would be easily confused because these steps were never based on anything they clearly understood. It was all a jumble of disjointed factoids. When solving word problems they would constantly ask me what operation they should use and, when they worked through the problems, “Is this right, teacher?” I was the sole arbiter of right and wrong. Students had no sense of how to verify if an answer is even close to being possible.
It never occurred to me that my students have knowledge they had never been formally taught. Fortunately, one day I came across a professional development article about Cognitively Guided Instruction (CGI.) The main premise was that you could give students word problems and support materials (manipulatives, 100 charts, etc.), and by facilitating questions guide them in using their prior knowledge to solve problems they had never seen before. I saw students solving 28 + 37 without any formal instruction on regrouping. Some students would count on from 28 using counters while others would model 28 and 37 with base 10 blocks and add the tens then the ones, then combine the partial products:
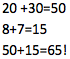
I’m fortunate enough to still work on how best to engage students to making sense of math by solving challenging problems. I work in the professional development department at MIND Research Institute designing workshops and lessons to integrate ST Math into classroom instruction. Although I brought much field experience to this job, I have gained a deeper understanding about how the human brain learns and acquires new information. When solving a new or novel problem, like the ones found in ST Math, students draw on their previous knowledge to create a hypothesis, test it, and then adjust their schema (or reinforce it) based on the outcome of the problem. I see this happening dozens of times as students work through ST Math puzzles during a session on the program.
Each time I visit schools I am reminded of students innate ability to learn by applying prior understanding to new situations and seeing the consequences of their decisions. When we intervene too quickly with students struggling on a problem, we are undermining their innate ability to learn. Students quickly begin to rely on us to give them answers rather than work through problems and, by persevering, figure things out for themselves.
While working as a math coach at a Title 1 schooI, I gave first through fifth graders a non-routine problem to solve. Students had access to manipulatives and were encouraged to show their thinking with pictures, numbers/symbols or manipulatives.
Problem: There are cows and chickens in the pasture. The farmer counted eight heads and 22 legs. How many chickens and cows are in the pasture? (First and second graders used five heads and 14 legs).
Here is one trend I observed:
Many first and second graders used pictures to solve the problem. This first grader made five cows then traded one cow for a chicken until the number of legs worked out.
Many fourth and fifth graders stumbled with the problem often applying procedures they have previously learned but not knowing how to apply them to the situation.
This, I fear, is a student who has always been taught but never really learned deeply. Students in these situations will likely stumble in more advanced math, not to mention in Common Core standards.
I can’t imagine not teaching with non-routine problems to see how students use their prior knowledge, and then tailoring the lesson to advance them on the road to higher math. This, at least, will prevent children (and adults!) from assenting to “utter nonsense.”
Erich Zeller is the Instructional Designer for the Product Team at MIND Research Institute. Follow him on Twitter @ErichZeller1.
.png)
Comment