
Since the big shift in math standards, mathematical coherence is a phrase that can be found accompanying most state standard lists and guidelines. Essentially, it’s telling educators that students should be connecting mathematical concepts to one another instead of learning procedures in isolation.
In other words, mathematical coherence is another way to say conceptual understanding in math. At MIND, we define conceptual understanding as the creation of a robust framework representing numerous and interwoven relationships between mathematical ideas, patterns and procedures.
In the visual instructional program ST Math, coherence is built through active exploration of visual models that connect concepts to one another. In the example below, students learn addition and subtraction with the same visual model that later introduces fractions.
Seeing a familiar puzzle presenting a new concept helps students understand that both concepts are part of a bigger whole (the number system) and takes the fear out of learning something new and tricky!
The Pie Monster first shows up in the subtraction module of the first grade objective “Adding and Subtracting Within Ten.”
Click here to see more ST Math addition and subtraction games.
The objective of the game (and all ST Math games) is to get JiJi across the screen. The consistent goal that is embedded across all levels and games, helps students focus on problem solving instead of rushing through the math for an extrinsic reward.
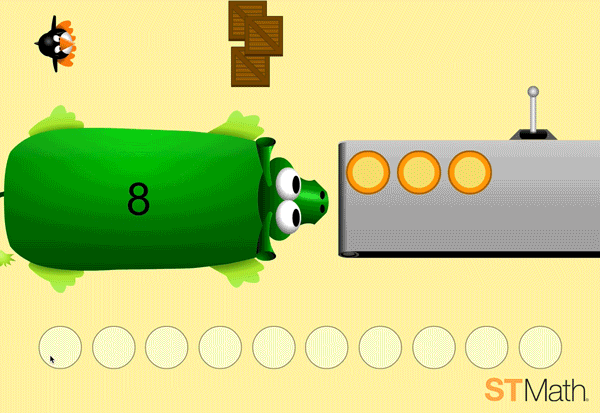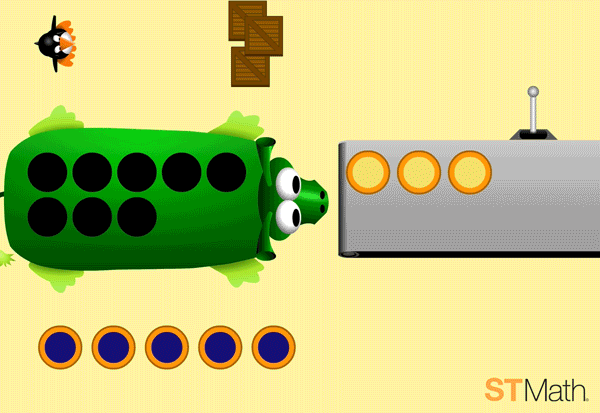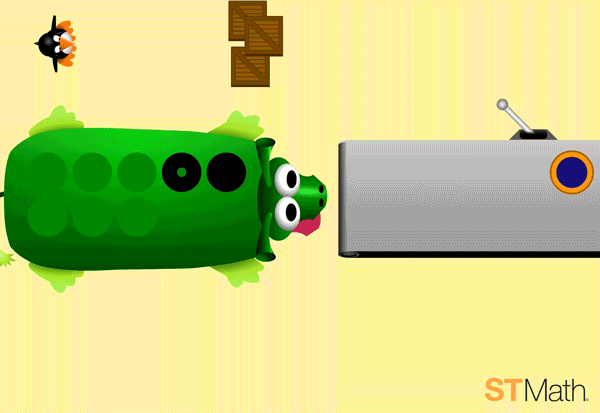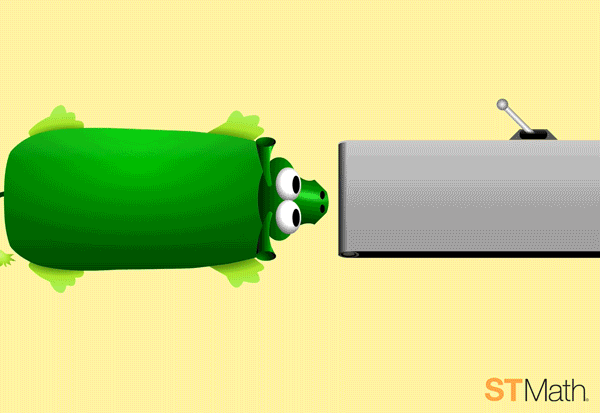
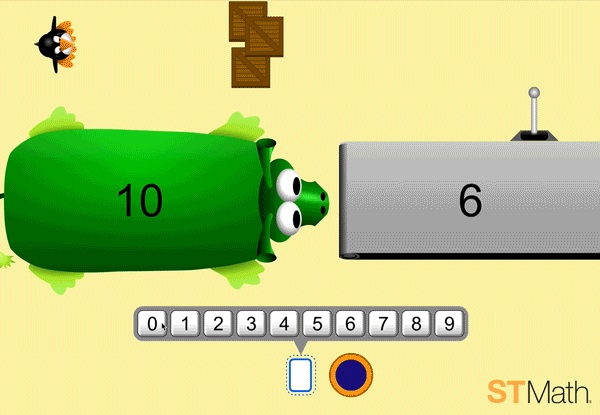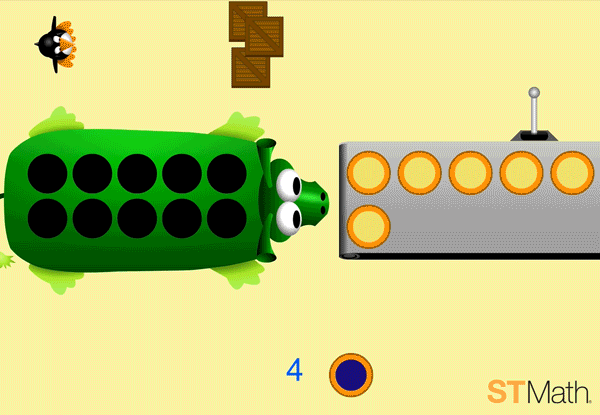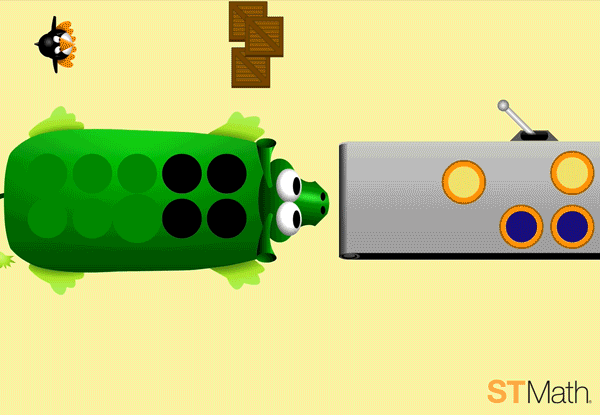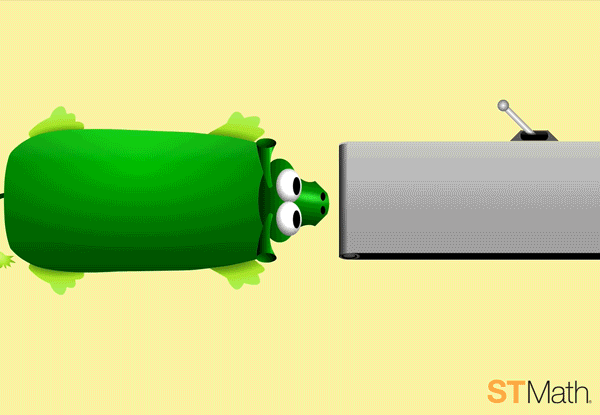
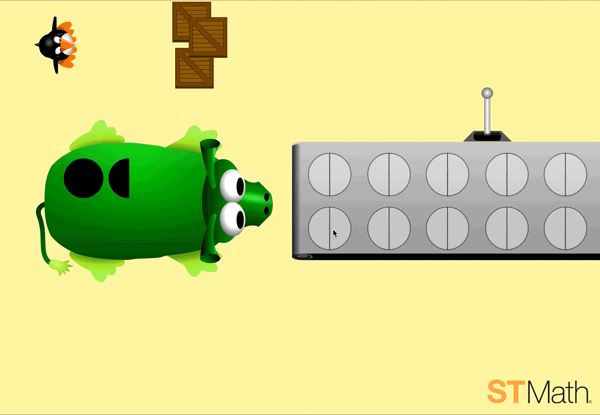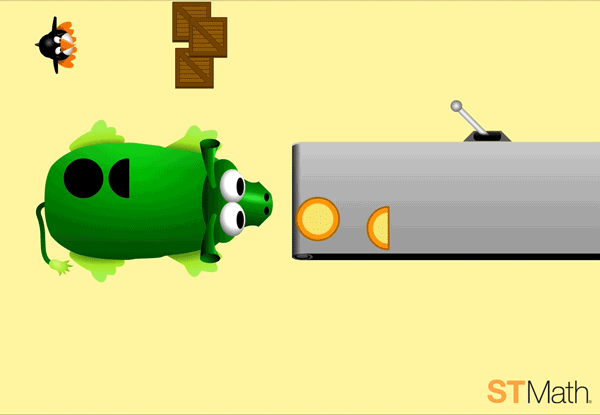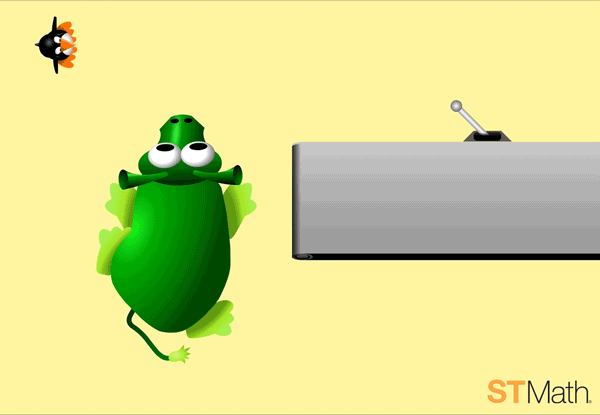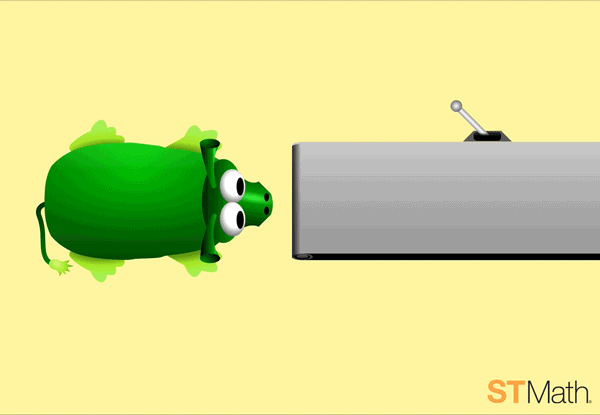
What do we notice about the first screen in Pie Monster? There are three sets of circles (pies) and the student has to figure out the relationship between the three sets to get JiJi across the screen.
In the example below, note how the pie monster and conveyor belt are both ten frames, and the circles on the bottom also add up to ten. The ten frame, which features prominently in previous addition and subtraction puzzles, as well as most core curricula, provides students with context (coherence) when problem solving in new settings.

Just by looking at the puzzle above, can you define the question that is being asked? How would you solve it? Is there a different way from the one that first occurred to you?
A common answer, especially to someone already familiar with equations and subtraction, is a subtraction equation. This puzzle asks for the difference between the number of circles on the pie monster and the pies on the conveyor belt.
But students might not immediately see it that way! They could approach the problem by counting the circles on the pie monster’s back, counting the circles on the conveyor belt and adding extras to make it equal.
Leaving room for different strategies allows students to make connections between addition and subtraction, especially if teachers take the opportunity to explore those strategies and ask students to explain their thinking.
Click here to get facilitating questions for ST Math.
In further levels, the circles are replaced by numbers, but the animations still show their representations, reminding students of the relationship between the concrete and symbolic. This reinforcement of the connections between a concrete count of objects and their symbolic representation supports students’ development of number sense.
In the final level, all three sets of circles are replaced by numbers but the problem still doesn’t explicitly show how the numbers relate to one another with add, subtract or equal signs. It’s up to the student to problem solve using the animations and their conceptual understanding of what is going on in the puzzle.
Pie Monster’s next appearance is in a third grade objective called “Fraction Concepts” which introduces fractions visually, without ever jumping into notation.
The setup of the game is very similar to Pie Monster in first grade but there are a few notable differences. The circles at the bottom are all gone which means students have to make their selections right on the conveyor belt, and the monster is a lot smaller with a maximum total of six instead of ten.
In the first few levels, the game asks students how many pies does the monster need? They need to match the conveyor belt with the circles they see on the monster:

Once students are familiar with the mechanics of the game, fractions come out to play. The game concept doesn’t change, but instead of matching whole pies with whole pies, students select the equivalent by halves.
A key learning moment in these first levels is how the ten frame of pies on the conveyor belt are now shown as two halves of a whole, but the Pie Monster shows wholes or stand-alone sections.
Similar to how we would show ½ as a fraction, but 2/2 would be simplified into 1. Returning to this puzzle and asking students to explain how they understand the difference can help make connections to fraction notations later on.
Once students master halves, the levels present the pies in thirds:
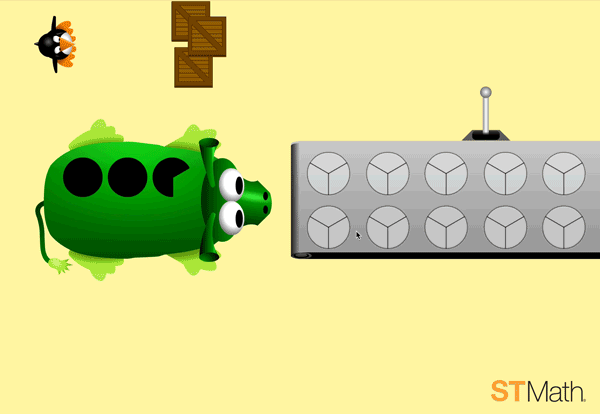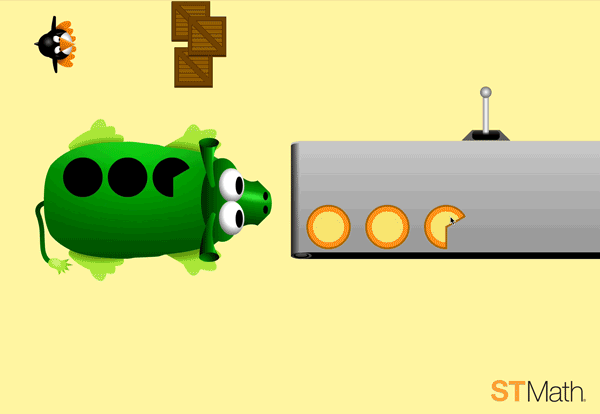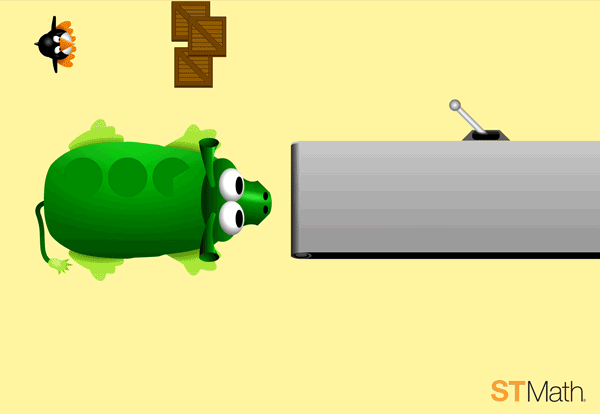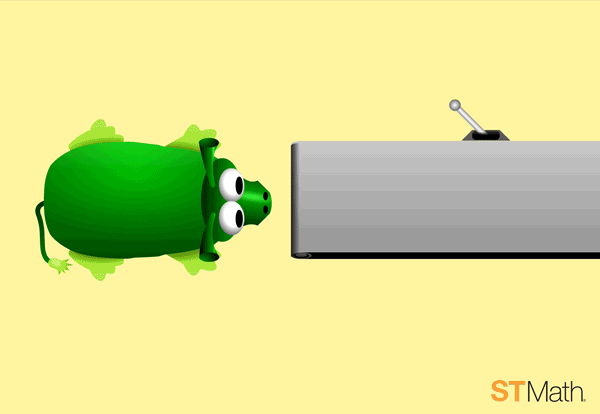
By level three, students start to build understanding of adding fractions by selecting enough pie pieces to accommodate two monsters:
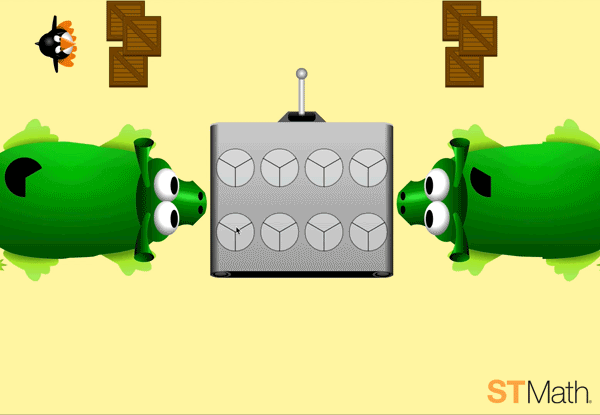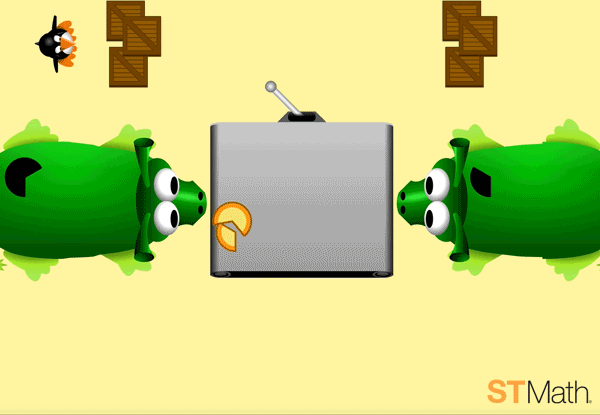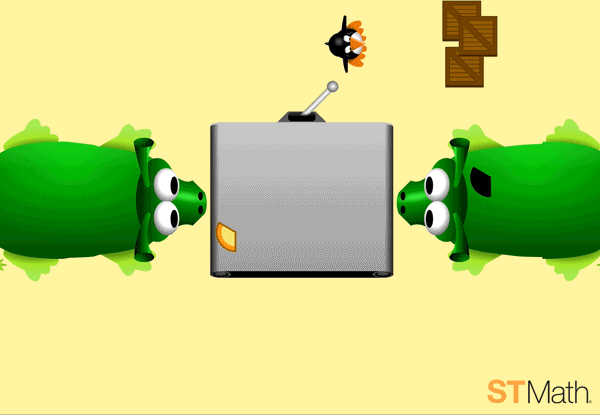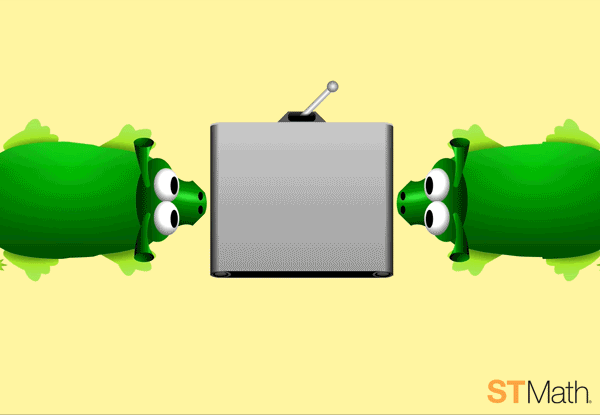
Through all three levels, students explore fractions with various denominators in a framework that already makes sense to them. This way, fractions are not a brand new and separate thing, but a natural extension of what they already know and understand in number operations.
If you liked this dive into Pie Monster, check out our other game highlights:
Or play some ST Math games for yourself!

Ieva Galinyte is an associate product manager at MIND Research Institute. She enjoys writing about and keeping up with the latest trends in math education.
Comment