Some years ago, there was a shift in the prevailing paradigm away from focusing on individual skills to emphasizing a more conceptual understanding.
However, despite this change in thinking, we continued with business as usual, using pacing guides based on individual standards and exams focused on those standards. We often found that there was not enough time in the day to teach each standard conceptually, which led to frustration in trying to explain more with less time or content support. As the focus shifted towards conceptual understanding, it became noticeable that adults were talking more and the students were doing less.
A glimpse at the answer lies in our desire to explain concepts well enough that kids “get it” and are able to “see” the mathematical idea quickly and effortlessly. We want our explanations to be so effective that kids grasp the concept immediately. Then, if kids could see how math is easy, they’d like it more.
This creates a vicious cycle where adults must put extra effort into explaining concepts in order to make it easier for kids to understand. There is a pressure to make math enjoyable and to ensure that kids grasp concepts almost instantly to meet educational standards. At the same time, we have to contend with ideas like productive struggle and the value of mistakes. It feels like a tug of war constantly pulling us in opposite directions.
The brain is a connection-making machine. It inherently seeks out opportunities to build or forge connections—think of a toddler’s curiosity. We enjoy finding even subtle connections between things, like rhymes or puns, because our brain is constantly looking for ways to connect and process information. We are constantly searching for new ideas and new connections between ideas. This is useful for us because it makes ideas easier to process in the brain and easier to use in the world around us. Highly complicated skills like tying our shoes or understanding what 5+7 means went from being a challenge (new and unconnected) to being second nature (highly connected and automatic).
Neuroscience usually calls these ideas schemas. They act as a map in the brain of an idea (a city) and connections to other ideas (roads between cities). And, just like roads, schemas are meant to be used. If an idea has no connections to other ideas, it will fade away and be forgotten—like cities along the old Route 66 that became ghost towns. In the same way, lifeless ideas are forgotten. Ideas that didn’t take any travel time to get to aren’t as valuable and also not often remembered. This is an analogy as to why the more we explain, the more we see kids forget. The brain doesn't just store information like a computer—it needs meaningful connections to make knowledge truly meaningful and useful.
A new paradigm is emerging that aims to empower us by focusing on big ideas.
Big ideas can be thought of as interconnected concepts or schemas that students can deeply understand and apply. While traditional standards are typically covered in a short period of time, Big ideas are explored throughout different grade levels and can continue to be relevant in advanced studies. These foundational concepts in elementary school are enduring and provide a strong basis for future mathematical explorations.
Here’s an example: Most of elementary school is built on generalizations or abstractions centered around a single big idea.
How many dots do you see? And how do you know?
We can count the total number of objects without actually counting one by one.
Until you begin to build the schema of counting without counting, it feels like magic to know the answer quickly. This is why kids benefit from so much counting early on—they learn to trust that counting one by one is not the only way to solve problems. A significant focus of Kindergarten is to build the foundations for this big idea—one that is tricky to unpack if we only teach to individual standards.
In early grades, this big idea is further explored through subitizing (counting small amounts by inspection), counting on (starting the count sequence part way through), etc. As another example, many states already recognize the connection between addition and counting in early grades. That’s big ideas-esque because addition starts off as another way to count without counting.
Here’s one more. When given a large collection to count, grouping is particularly helpful. Enter place value: the way in which we record the count of objects when we count by grouping. If we agree to group objects by tens and knowing how to represent ten groups of ten, counting large collections—like the one's below—becomes more manageable. It would be nearly impossible to count one by one, given the overlaps.
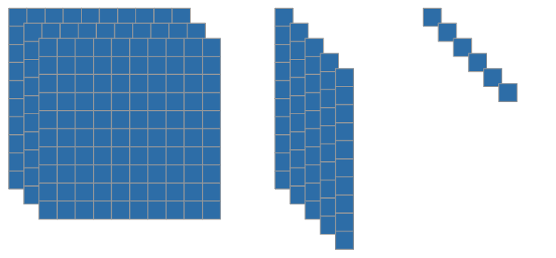
On the surface, it’s a different question than the one with dots. But in the context of big ideas, it’s the exact same idea played out in two different examples.
Once counting tens repeats the same problem as counting a bunch of ones, we can simplify the process by grouping numbers into hundreds, thousands, and beyond. This approach introduces a key concept of combining and breaking down numbers, known as composing and decomposing, which is fundamental for understanding place value, shapes, fractions, and other mathematical concepts. We can put together or take apart as a strategy to count without counting.
This marks a departure from traditional educational methods, since it promotes an engaging and active construction of highly transferable and immensely connected schema—or big ideas. Standards speak to big ideas, but they aren’t big ideas themselves. As the new California frameworks suggest, standards provide guidance on implementing big ideas but do not constitute a full curriculum.
The shift from teaching to standards to teaching to big ideas is underway.
A few states are taking a bold stand on the value of teaching big ideas. While this trend has been in conversations and many of our wishes and dreams for a while, California and Georgia are calling them out by name. Georgia, in their new standards, and California, in their recently adopted frameworks. Both states speak to the value of big ideas and are beginning to unpack what it means to teach big ideas.
So, rather than being a buzzword that sounds great but comes with little in the way of implementation, big ideas may very well prove to be a pivotal moment—and necessary jolt—in education because it’ll bring with it enough pragmatic implementation guidance so that we aren’t leaving classrooms hanging when it comes to how to teach to big ideas.
While the term big ideas is more recently coming into vogue, MIND spent the better part of three decades dedicated to building sticky, conceptual schema. Through the early years of the 2000s, we were rapidly iterating our program to crack the code on teaching big ideas (schema) and, by 2010, had accumulated enough years in the trenches that the mistakes, successes, and productive struggles of the prior 15 or so years began from a reputable, replicable, scalable solution. For the past decade-plus, we’ve been able to show results at scale across the widest possible range of student demographics and states.
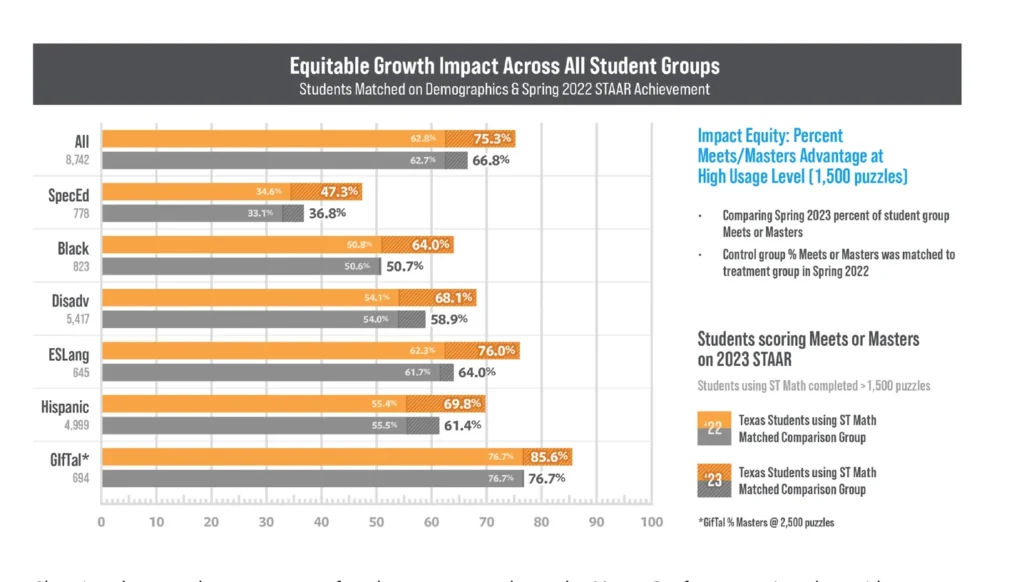
This has cemented the idea for us that teaching to big ideas is not only a great thought exercise. When implemented well, it’s a game changer across the board.
Get ready to unpack the big ideas in our upcoming blogs and share our passion for why this is such an exciting time in mathematics education.
Brandon Smith is the Lead Mathematician and Product Director at MIND Education, where he specializes in mathematics within ST Math and MathMINDs. Through his expertise, Brandon develops interactive learning experiences that foster a deep understanding and appreciation of mathematical concepts, utilizing a learning-by-doing approach. He is also dedicated to promoting equity in learning and development within the field of math education.
.png)
Comment