
Teaching statistics is hard. For one thing, stats activities often take a long time to do. Also, for any grade level, the relevant stats activities are often a combination of different math activities. Even something simple, like building a line plot of a simple bell curve, can consist of making dozens of measurements and plotting them all as points over a number line. Just one stats activity can be the same amount of work as an entire math worksheet!
How can we best utilize the amount of time teachers and students have in the classroom for interactive stats activities? As a game designer at MIND Research Institute, I was excited to answer this question. I have spent the past year applying game mechanics to statistics in a way that ensures students could build line plots and receive informative feedback much faster than in a traditional classroom activity.
Line plots (or dot plots, as they’re also known) are a building block on the way to more sophisticated visual representations, and are most commonly introduced in second grade. I apologize to all the eight-year-old blog readers who are already familiar, but here’s an example line plot:
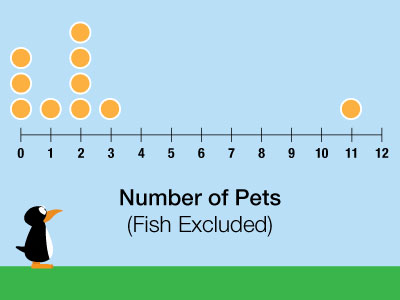
In this example, I asked ten of my colleagues how many pets they had. As you can see, I didn’t count fish (because you can’t cuddle a fish, or at least you shouldn't). At the extremes, you can see that three people had no pets, and one person had eleven pets (which frankly explains a lot about him).
This kind of thing is exactly what second graders are expected to do. Eventually, this will lead to all the usual suspects for stats—normal distributions, standard deviations, and the like. For second graders, though, we are asking a lot of students. The number line is a new concept, and in this example the number line needs to have ten different measurements plotted accurately above it.
Here’s the relevant Common Core standard, for those of you who, like me, like to decipher standards for a living:
CCSS.MATH.CONTENT.2.MD.D.9
Generate measurement data by measuring lengths of several objects to the nearest whole unit, or by making repeated measurements of the same object. Show the measurements by making a line plot, where the horizontal scale is marked off in whole-number units.
The “number of pets” survey is a great introduction to dot plots. After students create their line plots, the teacher could lead a discussion with questions like “What is the most common number of pets?” and “What is the most pets that anyone has?” These questions map nicely onto the concepts of mode and maximum.
The main downside to this activity is that it is missing a rigorous sense of measurement. Students at this stage should be making a strong connection between line plots, the number line, and rulers. In the survey, however, students are simply declaring numbers, possibly made up. Is Joey counting his iguanas as one pet instead of two? Is Natalia counting her imaginary unicorns? The measurement rigor is missing from this activity.
For another idea, let’s turn to one of my favorite resources for early statistics education, the “Guidelines for Assessment and Instruction in Statistics Education” (GAISE) PreK-12 Report by the American Statistical Association.
The GAISE Report suggests on page 31 (recommended reading, really!) that each student measure his or her arm length, and then the class makes a plot of all the lengths. The Common Core standard supports the use of rulers in this way, and the measurements could also include fractions for the slightly older students.
It’s still missing something, though: meaningful context. Meaningful context is the holy grail of any classroom lesson, to be sure, but statistics has an unusually high potential to actually achieve it. Who cares how long our arms are? And let’s not forget that having a noteworthy arm length could be a pretty embarrassing thing in the second grade (I for one wouldn’t have appreciated my second grade “monkey arms” being used as an example of an outlier in a stats lesson).
What can students measure that they actually care about? It needs to be something that represents a real effort, something that the student was trying to do. If enough students were trying to do something that could be measured, a teacher could make it into a line plot and observe the variability across students.
With this in mind, when our team got together to start building the brand new statistics games for the 2016 version of ST Math, I kicked it off with a line plot-building exercise. It could just as easily work outdoors at a school.
1. Set a jump rope on the grass to represent the goal line, and about 15 feet from it, set a bucket of golf-sized wiffle balls.
2. Mark distances from the batting spot (0 feet) to the jump rope (15 feet), and a bit beyond the jump rope (20 feet).
3. Split into two teams. A player on each team is designated as the pitcher, pitching wiffle balls to team members who use a racquet to try to hit the balls as close as possible to the jump rope.
4. After everyone has batted, measure the location of each ball for each team.
5. Back in the classroom, record the raw data on the whiteboard. As a class, create two different line plots, one for each team.
Creating two line plots allows for a great opportunity to compare and discuss as a class. Maybe start by asking "Who won?" It’s an easy question to ask, but not so simple to answer. Depending on the age of the group, it could lead to great conversations about mean vs median. Even for early grades, the mode could be used to discuss the “most common” distance. Depending on the age group, another great question is, “Who was more consistent?”, which in sixth grade can motivate boxplots and interquartile range (and mean absolute deviation, if you’re bold enough).
It was exciting for me, as an ST Math game designer, to explore the possibilities for bringing line plots into ST Math for the first time, and using technology to amplify what students can learn during interactive statistics activities. These all-class group activities are engaging, but they take a long time. Organizing a game like the one I’ve described requires about an hour to implement. In the same amount of time used by that group activity, students can make many line plots in ST Math. Similarly, class activities are great introductions, but even the most diligent teacher can’t possibly provide real-time feedback for every student as they all make line plots. But this is what ST Math does well, by giving just-in-time feedback for every student in the class.
Not familiar with ST Math? Learn more and play the demo.
In the case of line plots, I wanted the students’ first experience to be very similar to the ball-and-racquet game mentioned above. Students control JiJi’s friend Red Panda to kick a ball toward a goal, and then make the appropriate marks over a number line in order to make a line plot. Students have been asking me to make a soccer game for years, so I was excited to finally have the right mathematical context to do it. But I had one major design obstacle in front of me: how to handle the “goal.”
You see, one of the things that makes ST Math so effective is its relentless focus on education. The game rewards students based on what they’ve learned, and never on non-essential game elements that could distract students from the learning.
So here’s what we tried: if JiJi’s friend Red Panda kicks the ball to the goal, a creature pops out of the ground underneath it. If Red Panda kicks the ball that same distance again, a different creature pops out. If Red Panda misses the goal, nothing bad happens at all. Goal or no goal, the student still builds the line plot, and the game progresses based on the accuracy of the line plot, and never based on the kicking accuracy.
Here’s an example of a student taking only 2 minutes to create a line plot in ST Math:
When we tested at our first school, we found that the goal worked just as intended: students were delighted to see the surprising animation, and continued to aim for the goal, kick after kick. Furthermore, they built line plot after line plot, and when we asked follow-up questions that required interpretation of the line plots, students were able to answer the questions in the original context. Here’s a transcript from conversation with a second grade student about the dot plot that she built:
Researcher: “How many times did you kick to five?”
Student: “Oh my gosh! One, two, three… four!”
Researcher: “OK, how do you know that? How do you know you kicked it four times?
Student: “Because there are four dots.”
Researcher: “How many times did you kick it to two?”
Student: “Zero.”
This is exactly the kind of response we would hope for from a second grader. She was able to answer questions about an event by referencing the line plot that she made, and even demonstrated a solid understanding of zero as a measurement.
ST Math now includes many games about line plots. The soccer game is just one example, but it’s an important one, because it “kicks off” the topic in every grade level from second grade to middle school. Even in higher grades, the same context can be used to ask more challenging followup questions. For example, after enough students have played the Mean Absolute Deviation game (a remarkable game in its own right), the Soccer Dot Plots game can be used in class to ask students to compare the two line plots:

Paul Blair is Director, Product - ST Math Platform, at MIND Research Institute. The content in ST Math features seven of Paul’s game designs, all focused on early statistics.
Comment