Our math education system is at a crossroads. The traditional approach of teaching through memorization and rote procedures is no longer sufficient in preparing students for the complexities of the modern world. We need a major shift towards fostering genuine understanding and critical thinking. Last week, I experienced a vivid reminder of this necessity when I asked my 7th-grade son about his Algebra 1 class. They've started a unit on quadratic equations and are factoring polynomials.
"Why?" I asked.
"Don’t know," he replied, “but there’s this rule we have to use."
I knew where he was going with this.
"No area models, no algebra tiles, no drawings?" I asked.
"Huh?" he said.
That told me all I needed to know, so we had an impromptu math lesson in the car on the way to soccer practice.
What made all of this even worse was that the next day he came home and told me, “You know that rule we did yesterday? Today they told us it no longer works and we have to use a different rule with these new equations.”
Learning math through arbitrary rules, disconnected from any existing schema, works completely counter to the way our brains actually learn. It also turns students off from mathematics as a subject and ignores the creative problem-solving needed for future careers. It’s void of why students should care enough to dig deep and think beyond memorization or passing the test. Arguably, the saddest loss is mathematics then becomes something students dread and never fully understand for its fascinating—and beautiful—role in human innovation.
In My Daughter Doesn't Need my Mother's Math Education, we discussed how our kids don’t need our grandmother’s approach to math—the algorithmic thinking and memorization approach no longer best serves future problem solvers. Now, we must teach students how to use creative and critical thinking to solve non-routine problems, leaving behind the narrow “answer-getting” legacy of the Industrial Revolution.
Algorithmic thinking, or answer getting, is still the dominant mathematics teaching method in the United States, presenting students with a math problem, providing a solution method for it, and following up with extensive practice (Hiebert, 1999, 20003). The perception is that it saves time, prevents miscalculations, and the skills apply to most school textbook problems (Jonsson et al., 2014, 2016; Norqvist, 2018). But given the demonstrably low math scores nationwide and recent research, it limits student learning (Carpenter, et. al, 1998; Hiebert & Wearne, 1996) and discourages a deeper understanding of math principles. So, students, like my son in his algebra class, superficially do work without any conceptual understanding of why or how to apply it beyond the problem at hand.
There is another way. In 2014, researchers made an apples-to-apples comparison. The students who had to struggle through and creatively find their solutions not only performed better, retained their knowledge and outperformed again when asked to reconstruct the work one week later (Jonsson et al., 2014). Further, students who had to find creative approaches registered different brain activity than those with algorithmic thinking, remembering the information more easily. (Karisson Wirebring et al., 2015).
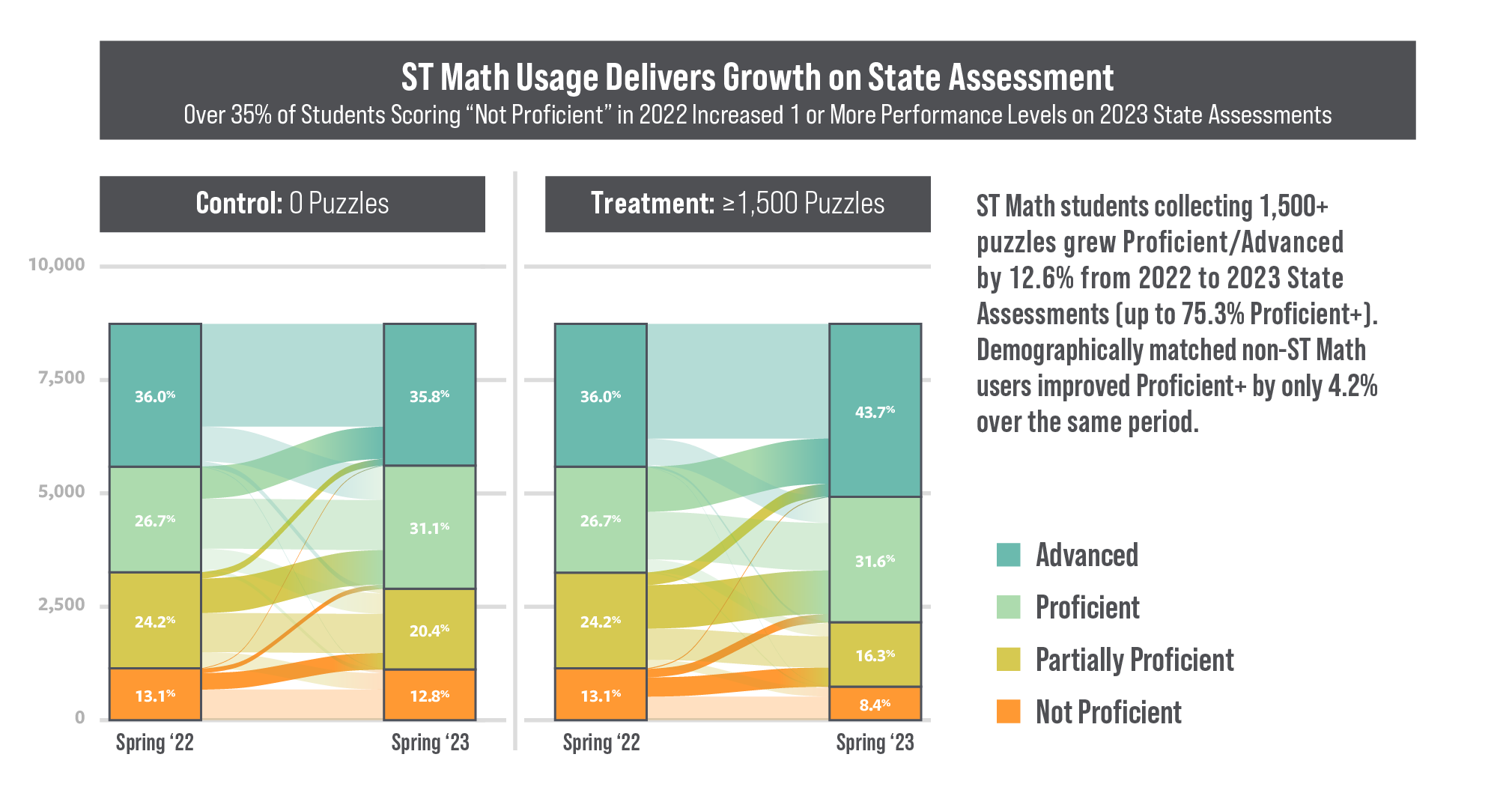
Study after study demonstrates students theoretically learn more by doing, by being active learners rather than passive receivers of knowledge. But does this approach work in the classroom? Can it work at scale? In Texas, the results were clear. The Texas Education Agency (TEA) made ST Math, a visual math program that uses a game-based, creative reasoning approach, freely available for all Texas students, and then tracked STAAR Math performance growth. Forty-eight percent of students who used ST Math dramatically improved, and remarkably, students at Did Not Meet levels decreased to near elimination. Also, ST Math and creative reasoning helped all students, even English Learners and Special Education students.
So we know creative reasoning works, why isn’t it more evident in classrooms? Why is my son’s algebra 1 lesson still using the same rules and procedures for solving quadratic equations like it’s still 1954? It’s a combination of the legacy of old teaching methods and our societal aversion to letting students struggle, and systemic challenges. Facilitating students as they creatively figure things out is much harder to do than delivering a similar lesson via direct instruction. Managing a classroom where students are engaged in a process of discovery requires letting it get messy but being able to bring it back to focus quickly. It also needs a deep conceptual understanding of mathematical concepts so that the teacher can help guide students to the desired learning no matter where they end up, and it needs a teacher who is very comfortable leading students with questions rather than giving answers.
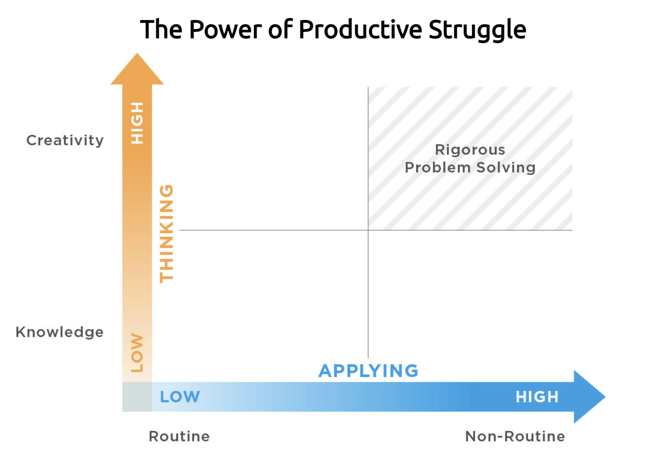
Neuroscientific research proves meaningful, lasting learning stems from productive struggle. This doesn’t mean students are left figuring things out without teacher support or tackling things beyond their ability. We recommend “making sense of mathematical problems that are just within students’ reach of understanding as opposed to simply memorizing a presented solution (Hiebert & Grouws, 2007).” Students work more actively to make sense of a situation, forming “better connections to knowledge they already possess.” (Hieber & Grouws, 2007). When this happens students can apply what they’ve learned to solve bigger, modern problems, like how to capture solar energy to power a car.
Teachers have a pivotal role as change agents. Students become more motivated to learn and stay engaged when they feel valued and connected to their teacher. That means when things get tough and struggle happens, teachers help build resilience, open space for “more high-impact teaching practices”, and environments where creative reasoning can thrive.
I wish that my son’s math class was conducted with the same passion, verve and “learn-by-doing” I observe at his club soccer training sessions. My “neuroscience-in-action” sensor is often on high alert as I watch the coaches skillfully allow kids to struggle, make mistakes, and immediately provide formative feedback asking them “what do you think you could have done differently? OK, now try that.'' Bringing this kind of active learning into math classrooms could be the change we need to inspire and educate future thinkers.
Learn more as we compare algorithmic teaching and creative reasoning in the classroom. Follow along as we explore transforming math education.
Nigel Nisbet is the Vice President of Content Creation at MIND Education, a non-profit organization dedicated to equipping all students to solve the world's most challenging problems. He is also the author of the E-book “I think, I try, I learn” and presenter of the TEDx talk “The Geometry of Chocolate."
.png)
Comment