During the breaks at a couple of recent professional development trainings, my colleagues and I asked teachers to share their definition of “deep conceptual learning.” Common threads ran through the individual responses. Teachers agreed that deep conceptual learning involves:
At MIND, deep conceptual learning is as common a topic of conversation as it is in schools. While basic procedural skills like counting and computation are critical, they are just the tip of the iceberg.
When I was a kid, we primarily learned math through computation and memorization. We did word problems, but these didn’t require much thinking. “If Jane has three cookies and Spot takes one from her hand, how many cookies does Jane have left?”
I distinctly remember the moment when I needed to shift from procedural to conceptual thinking – not that I knew that this is what I was doing at the time.
It was 1970-something, and we didn’t have the common core standards that encourage teachers to teach conceptually. Not to say that they didn’t – Mrs. Evans, my first grade teacher, most certainly did. But my third grade teacher wasn’t as strong in teaching conceptually. She could write the math on the chalkboard and correct us when we made an error in our rote math facts recall, but she couldn’t explain the concept behind the numbers.
Addition was simple. We added things to other things. If Sally gave Jane a cookie, Jane had more cookies. Easy. Subtraction was simple too. Especially since we called it “take-away” – exactly what Spot did to Jane’s cookie in the question above.
But multiplication? That was a new concept – a trickier concept. Confusingly to me at the time, when my teacher taught multiplication she didn’t say “multiply” she said “times.” I could tell time. I even knew that every number around the clock face meant that five minutes had passed. But “three times three equals nine” meant absolutely nothing to my young brain.
My teacher taught us to recite times tables. I had no idea how a table got into the mix, and why there was no clock involved in the times. I simply did not get it. I was frustrated, and it was the first time I ever felt lost in math. I tried to ask my teacher for help, but she told me to go back to my seat. I went home that day dejected and discouraged.
Fortunately, my mom was one of those moms who often asked “How was your day?” when I got home from school. On that particular day in third grade, I burst into tears. My Mom sat me down, listened, and then proceeded to explain that “times” meant “multiply” and “multiply is adding groups.”
Huh? Adding groups?
She showed me with some walnuts from the trees in our yard. Three walnuts in this group, three walnuts in another group, and three more walnuts. How many walnuts? Nine! Oh, adding groups! I got it! My mom taught me the concept that my teacher was unable to explain.
My Mom was quick to grab a bunch of walnuts to teach me the concept of multiplication. We can do the same for our children at home. The way we pose questions allows our kids to apply procedural or conceptual thinking to everyday problems.
For example, if you were to ask your six-year-old to help you set the table for dinner, you could ask in a myriad of ways:
Request 1 is very explicit and is a simple procedural application of a mathematical skill: counting. Your child is instructed on how many of each item to get and can count 7 forks, and then return to the drawer to count 7 spoons.
Request 2 is also a procedural application, though it can be achieved through multiple skills and thereby extends their application beyond simple execution of an explicit task. Your child could count and carry twice as in request 1. Or they could add 7 + 7, counting to 7 as they remove forks from the drawer, and then continuing to count to 14 while removing spoons from the drawer. Or they could pair each fork with a spoon as they take them from the drawer and count 7 sets.
Request 3 begins to introduce conceptual thinking. In this request, your child is given the explicit instruction to get forks and spoons plus information about the people their task will serve, rather than an explicit number of people. They must first conceptualize those people around the dinner table, and then equate that to the quantity 7. From there, they could apply any of the procedural skills described above.
Request 4 requires more conceptual thinking. It isn’t posed as a calculation or computation at all. Your child will first need to think about how many people were present at dinner the night before. Since their grandparent was present, the table will have 1 more than its usual base of 4. They’ll then have to consider that their aunt and cousin will join the table tonight and add those two additional diners. Then, they’ll have to think about which utensils might be needed. Lastly, they’ll have to go to the drawer and retrieve the appropriate quantity of different utensils.
By changing how the requests are phrased, you can move your child between procedural and conceptual understanding. You can do this in nearly any scenario. When I first started teaching math to my daughter, I didn’t ask her to add 2 + 3. I asked “If you have three jelly beans and I give you two more, how many will you have?” She responded instantly, “Five mama! Can I have five jelly beans?” She learned the concept that basic adding means “more” before she ever saw a plus sign. And, she learned it visually, precisely how ST Math teaches.
ST Math starts out each objective with visuals, without written numbers or symbols, building the conceptual before the procedural or computational. In this way, students learn more deeply.
We see evidence of this every time we’re in an ST Math classroom and a teacher introduces a new concept. The teacher frequently starts with the procedural and there’s always at least one student who excitedly declares, “Oh, we did this with JiJi (the penguin mascot from ST Math)!” The students see the concept come about in the symbols and numbers their teacher is presenting, sometimes even before they’ve gotten to the symbols or numbers for that objective in ST Math.
Students learn via trial and error. They apply learning from previous lessons – problem solving by attending to immediate feedback and taking that information into their own perception-action cycle. They explain, or engage in academic discourse, when they share with peers, talk about their thinking with their teacher, or participate in a small group or whole class lesson. With ST Math games that straddle grade bands, students relate the concepts they learned in prior years to new concepts.
In the first grade level of the ST Math puzzle “Bouncing Shoes,” students start by counting. Each ostrich has two legs and needs two shoes, each dog has four legs and needs four shoes. Two ostriches and three dogs need 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 shoes.
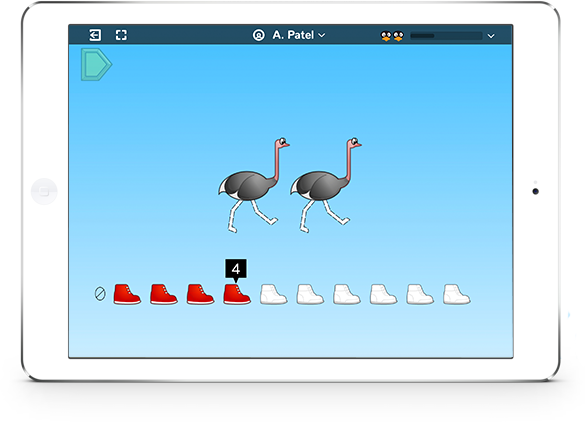St Math's "Bouncing Shoes" puzzle
When Bouncing Shoes appears again in second grade, students move from counting to adding: 2 + 2 + 4 + 4 + 4 = 16. Again, remember kids see the visuals of legs and shoes way before they see 2s and 4s and +s. They may start this game by counting, but the way the legs are offered in pairs and then pairs of pairs gets them thinking more deeply. They begin to see the groups of 2 or 4.
Students encounter Bouncing Shoes again in third grade when they begin to multiply. In the beginning, students often either group all the ostrich legs together and then multiply 4 x 4, or they split the dogs’ legs into pairs and multiply 2 x 8.
Play ST Math puzzles from grades 3-4 that build on multiplication and division.
Students can later use algebraic thinking to see this same problem as 2x + 4x = 16. They build upon their prior experience of seeing the legs and shoes as groups way back when they’re counting. By the time they get to pre-algebra, their minds are already steeped in the concept.
Great teachers like Mrs. Evans and ST Math do this for our kids in the classroom. But we can start them on that path before they start school and continue to support their learning as they grow.
Want the latest from ST Math? Sign-up for our ST Math newsletter and be the first to hear about our offers and announcements.
Alesha Arp is a senior user experience researcher at MIND Research Institute. When she’s not uncovering ways to improve experiences—at work, or IRL—she can often be found baking for family and friends. Homemade cakes are her specialty.
.png)
Comment