Some of our knowledge of the world is so well ingrained in us, that we don’t even have to think about it.
Consider a chair, for example. When we see a chair, we know immediately what it is and how to sit on it. We even know different ways to sit depending on if it’s a stool or an easy chair or a beanbag. And this is all automatic, without thinking about it.
Our brain has rich networks of information, called schemas, about chairs (and many other things). These schemas are created in the brain when we learn through the perception-action cycle. That’s what neuroscientists call the process in the brain where humans observe something in the world around them, decide to take action on their environment, and then perceive the results of that action.
We can kickstart the perception-action cycle in classrooms, and make it so that in math class, students know as readily what to do with a fraction problem as what to do with their desk chair.
To do so, students need to perceive the problem, take action and see the result of that action --- over and over again, strengthening the neural networks around that piece of understanding.
Manipulatives are a great way to put students’ perception-action cycle to work. And now, digital manipulatives are making it easier than ever to give students hands-on learning opportunities in class. Following are some real-world examples of how this can be done using ST Math’s interactive puzzles.
Second graders encounter two-step addition and subtraction problems for the first time in ST Math, not as a series of symbols and numbers, but as a situation where boxes are being pushed by a bulldozer. The scenario resembles activities often done with physical manipulatives like counting cubes. But in this case, digital manipulatives offer an advantage: individualized informative feedback for each student -- a type of one-to-one interaction that’s difficult to achieve with physical manipulatives in a classroom setting. Students
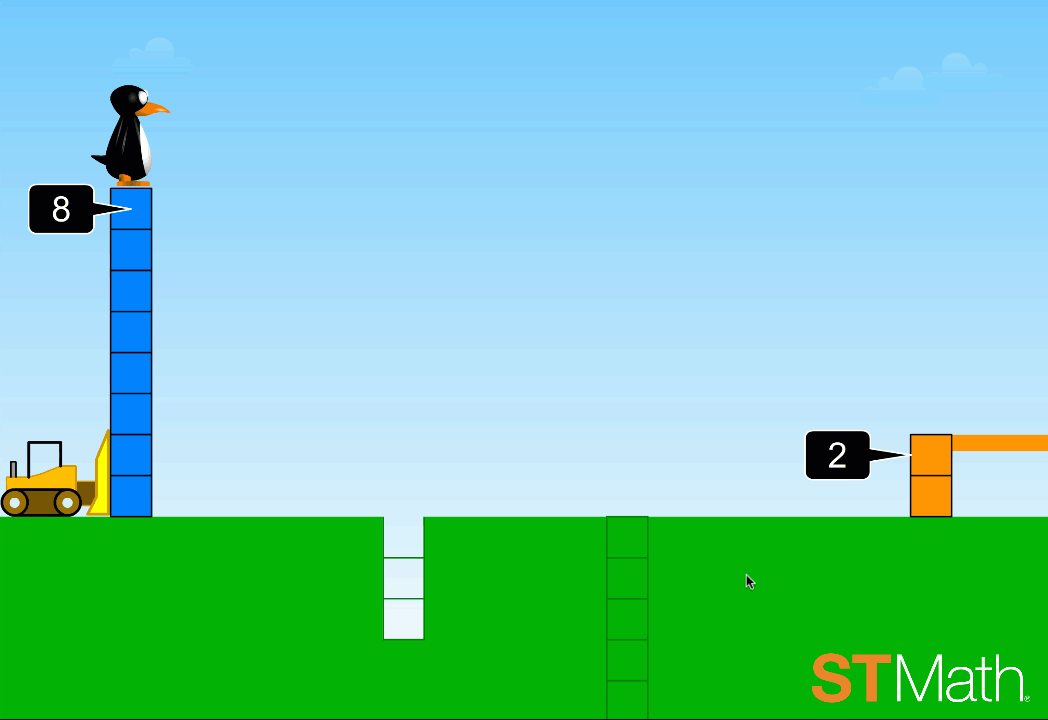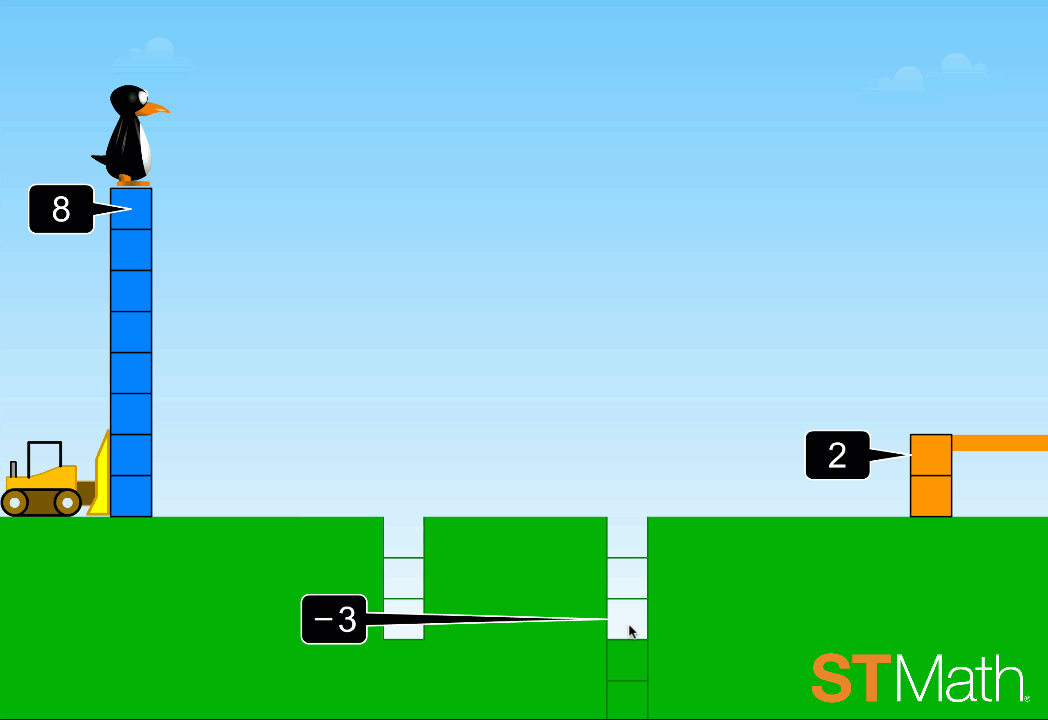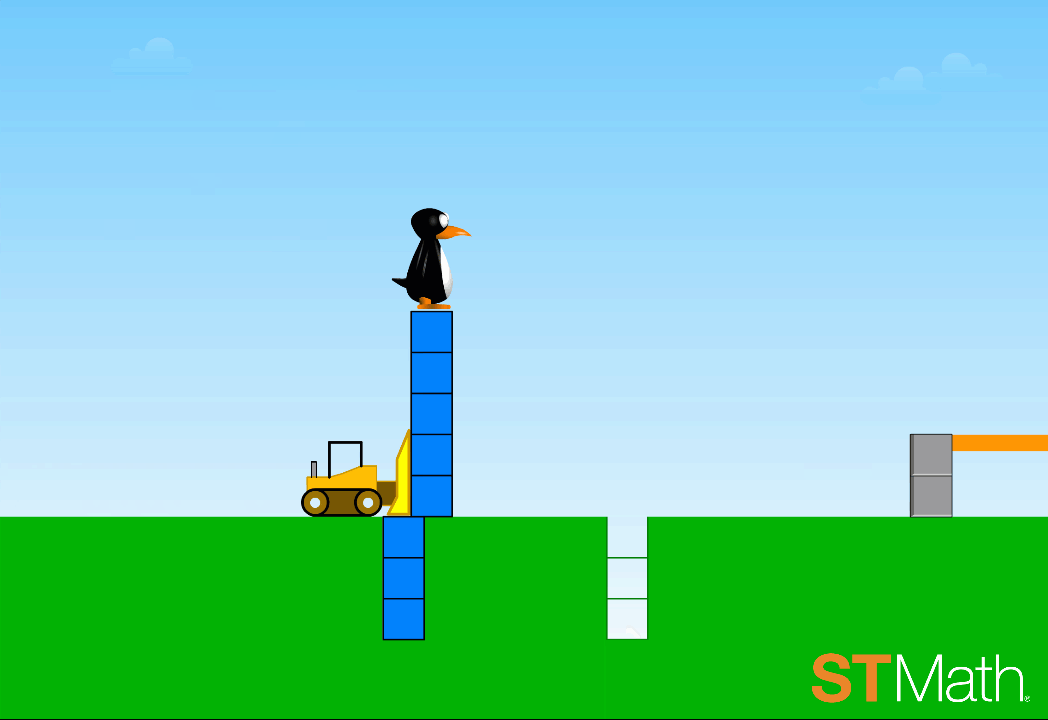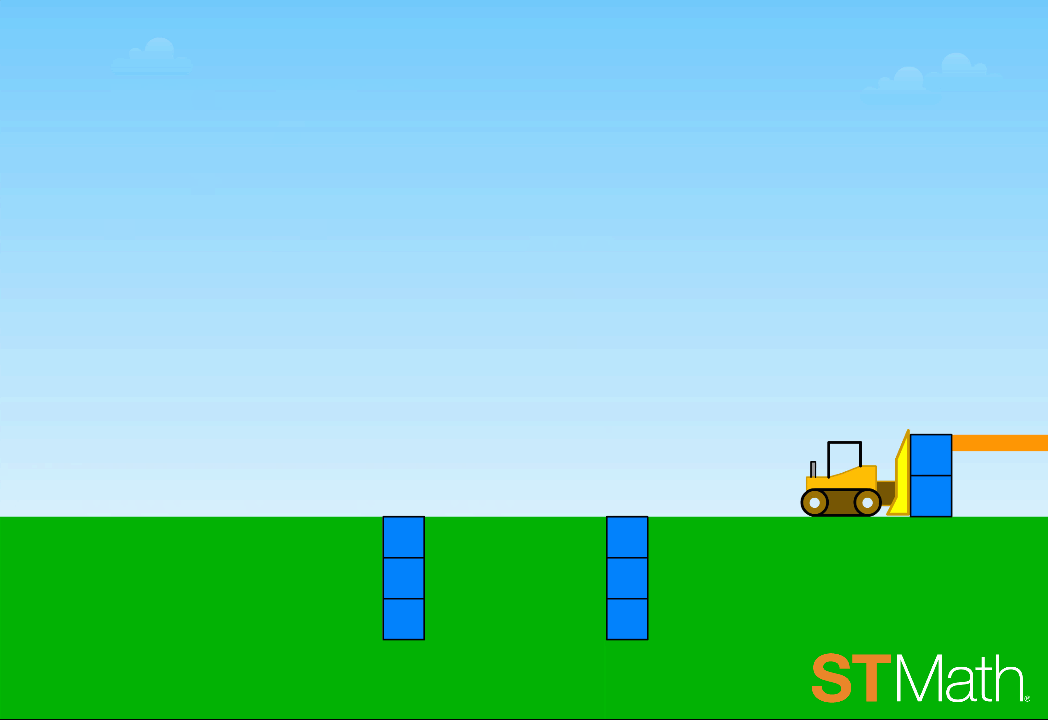
Addition and subtraction with fractions is notoriously challenging for many students. The JiJi Cycle puzzle puts two digital manipulatives in play -- portions of a circle that represent fractions of a whole, and a number line. Students
By invoking both the circles and the number line, the game fosters knowledge transfer between the concept fractions of a circle and a number.
Exponential growth is one concept that is nearly impossible to teach with physical manipulatives in a classroom because of the logistical burden. But digital manipulatives make it easy and fun to model exponentiation. In the middle school game Exponents, students
Digital manipulatives, like ST Math overall, allow students to see the math, take action, and perceive the results of those actions right away. Evoking the brain’s powerful learning mechanism, the perception-action cycle, creates strong schemas around mathematical knowledge. When students have deep, conceptual understanding of the math, their mathematical thinking comes more quickly and easily, allowing them to devote greater amounts of brainpower to the kinds of challenging multi-step problem solving that makes them successful not only in math class, but in life.
Christine Byrd writes about STEM and education issues for MIND Research Institute.
.png)
Comment